题目内容
2.将$y=sin(x+\frac{π}{3})$的图象上各点的横坐标缩短到原来的一半,纵坐标不变,再将图象上所有点向左平移$\frac{π}{6}$个单位,则所得函数图象的一条对称轴为( )| A. | $x=-\frac{π}{12}$ | B. | $x=-\frac{π}{6}$ | C. | $x=\frac{π}{6}$ | D. | $x=\frac{π}{2}$ |
分析 由条件利用y=Asin(ωx+φ)的图象变换规律,可得所得图象对应的函数解析式,再根据正弦函数的图象的对称性,求得所得函数图象的一条对称轴.
解答 解:将$y=sin(x+\frac{π}{3})$的图象上各点的横坐标缩短到原来的一半,纵坐标不变,
可得函数y=sin(2x+$\frac{π}{3}$)的图象;
再把所得图象象左平移$\frac{π}{6}$个单位,则所得函数图象对应的解析式为y=sin[2(x+$\frac{π}{6}$)+$\frac{π}{3}$]=sin(2x+$\frac{2π}{3}$),
令2x+$\frac{2π}{3}$=kπ+$\frac{π}{2}$,求得 x=$\frac{kπ}{2}$-$\frac{π}{12}$,k∈z,故所得函数的图象的对称轴方程为 x=$\frac{kπ}{2}$-$\frac{π}{12}$,k∈z.
结合所给的选项,
故选:A.
点评 本题主要考查y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.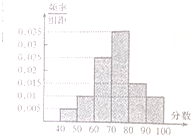 某中学为了检验1000名在校高三学生对函数模块掌握的情况,进行了一次测试,并把成绩进行统计,得到的样本频率分布直方图如图所示,则考试成绩的中位数大约(保留两位有效数字)为( )
某中学为了检验1000名在校高三学生对函数模块掌握的情况,进行了一次测试,并把成绩进行统计,得到的样本频率分布直方图如图所示,则考试成绩的中位数大约(保留两位有效数字)为( )
 某中学为了检验1000名在校高三学生对函数模块掌握的情况,进行了一次测试,并把成绩进行统计,得到的样本频率分布直方图如图所示,则考试成绩的中位数大约(保留两位有效数字)为( )
某中学为了检验1000名在校高三学生对函数模块掌握的情况,进行了一次测试,并把成绩进行统计,得到的样本频率分布直方图如图所示,则考试成绩的中位数大约(保留两位有效数字)为( )| A. | 70 | B. | 73 | C. | 75 | D. | 76 |
13.把复数z的共轭复数记作$\overline{z}$,复数z=3-i(i为虚数单位),则复数$\frac{\overline{z}}{1+i}$在复平面内所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.已知集合A={0,a},B={-1,1},若A∩B={-1},则A∪B=( )
| A. | {0,1} | B. | {-1,0} | C. | {-1,1} | D. | {-1,0,1} |
7.设f(x)=$\left\{\begin{array}{l}{{k}^{2}x+{a}^{2}-k,(x≥0)}\\{{x}^{2}+({a}^{2}+4a)x+(3-a)^{2},(x<0)}\end{array}\right.$,其中a∈R,若对任意的非零实数x1,存在唯一的非零实数x2(x1≠x2),使得f(x1)=f(x2)成立,则k的取值范围为( )
| A. | R | B. | [-4,0] | C. | [9,33] | D. | [-33,-9] |
14.已知i是虚数单位,则|$\frac{1-i}{1+i}$|=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |