题目内容
关于函数f(x)=sin(2x+| π |
| 3 |
①把函数f(x)的图象按向量a=(
| π |
| 12 |
②函数f(x)的图象关于点(
| π |
| 6 |
③函数f(x)的图象关于直线x=-
| 5π |
| 12 |
④把函数f(x)的图象上每个点的横坐标缩小到原来的
| 1 |
| 2 |
| π |
| 6 |
其中正确的命题序号为
分析:①由题意可得:即向右平移
个单位,即可得到y=sin(2x+
).②函数f(x)的图象的对称点为(
-
,0).③函数f(x)的图象的对称轴为x=
+
.④由题意可得:得到的函数为y=sin(4x+
).
| π |
| 12 |
| π |
| 6 |
| kπ |
| 2 |
| π |
| 6 |
| kπ |
| 2 |
| π |
| 12 |
| π |
| 3 |
解答:解:①把函数f(x)的图象按向量a=(
,0)平移,即向右平移
个单位,即可得到y=sin(2x+
),所以①错误.
②函数f(x)的图象的对称点为(
-
,0)(k∈Z),所以②错误.
③函数f(x)的图象的对称轴为x=
+
(k∈Z),所以当k=-1时,对称轴为x=-
,所以③正确.
④把函数f(x)的图象上每个点的横坐标缩小到原来的
,得到的函数为y=sin(4x+
),所以④错误.
故答案为③.
| π |
| 12 |
| π |
| 12 |
| π |
| 6 |
②函数f(x)的图象的对称点为(
| kπ |
| 2 |
| π |
| 6 |
③函数f(x)的图象的对称轴为x=
| kπ |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
④把函数f(x)的图象上每个点的横坐标缩小到原来的
| 1 |
| 2 |
| π |
| 3 |
故答案为③.
点评:解决此类问题的关键是熟练掌握正弦函数的有关性质,以及函数图象的平移变换原则.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
已知函数f(x)=
,关于x的方程f(x-1)=k(其中|k|<1)的所有根的和为S,则S的取值范围是( )
|
| A、(-4,-2) |
| B、(-3,3) |
| C、(-1,1) |
| D、(2,4) |
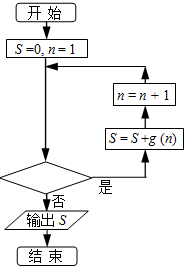 (2012•杭州二模)已知函数
(2012•杭州二模)已知函数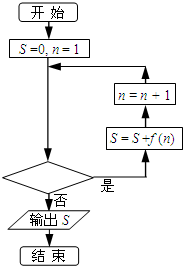 (2012•杭州二模)设函数
(2012•杭州二模)设函数