题目内容
已知数列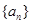 满足:
满足: ,定义使
,定义使 为整数的
为整数的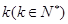 叫做希望数,则区间[1,2013] 内所有希望数的和M=( )
叫做希望数,则区间[1,2013] 内所有希望数的和M=( )
| A.2026 | B.2036 | C.32046 | D.2048 |
A
解析试题分析: =
=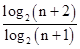 ,(n∈N*),
,(n∈N*),
∴a1•a2•a3…ak=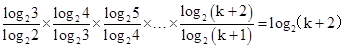 ,
,
又∵a1•a2•a3…ak为整数
∴k+2必须是2的n次幂(n∈N*),即k=2n-2.
∴k∈[1,2013]内所有的幸运数的和
M=(22-2)+(23-2)+(24-2)+…+(210-2)
=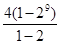 -2×9=2026,故选A。
-2×9=2026,故选A。
考点:本题主要考查换底公式、累乘法及等比数列前n项和公式。
点评:中档题,作为新定义问题,关键是理解题意。本题综合性较强,对考查学生综合应用数学知识的能力有较好的考查。

练习册系列答案
相关题目
数列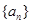 的前
的前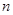 项和为
项和为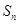 ,若
,若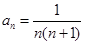 ,则
,则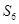 等于
等于
A.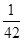 | B. | C. | D.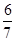 |
数列 的通项公式
的通项公式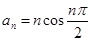 ,其前项和为
,其前项和为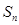 ,则
,则 等于( )
等于( )
| A.1006 | B.2012 | C.503 | D.0 |
数列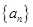 的通项公式
的通项公式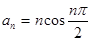 ,其前
,其前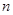 项和为
项和为 ,则
,则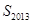 等于( A )
等于( A )
A.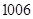 | B.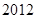 | C. | D. |
一个平面将空间分成两部分,两个平面将空间最多分成四部分,三个平面最多将空间分成八部分,…,由此猜测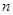 (
( )个平面最多将空间分成 ( )
)个平面最多将空间分成 ( )
A.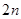 部分 部分 | B.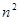 部分 部分 | C.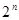 部分 部分 | D.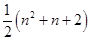 部分 部分 |
已知数列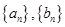 满足
满足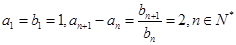 ,则数列
,则数列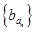 的前10项和为
的前10项和为
A.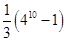 | B.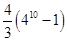 | C.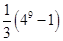 | D.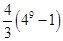 |
 的图象在点
的图象在点 处的切线的斜率为3,数列
处的切线的斜率为3,数列
 项和为
项和为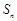 ,则
,则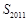 的值为( )
的值为( )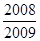



 中,
中,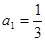 ,前
,前 项和
项和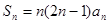 ,则数列
,则数列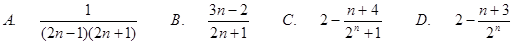
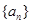 与
与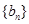 满足
满足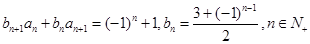 ,且
,且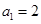 ,设数列
,设数列 项和为
项和为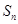 ,则
,则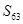 =.
=.