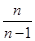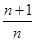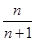题目内容
数列 的通项公式
的通项公式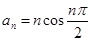 ,其前项和为
,其前项和为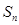 ,则
,则 等于( )
等于( )
| A.1006 | B.2012 | C.503 | D.0 |
D
解析试题分析:根据数列 的通项公式
的通项公式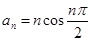 可知当n=1,2,3,4,得到的项为0,-n,0,n,依次后面的项周期出现,那么可知
可知当n=1,2,3,4,得到的项为0,-n,0,n,依次后面的项周期出现,那么可知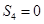 ,那么对于2013=
,那么对于2013=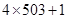 ,可知其和为首项0,故答案为D
,可知其和为首项0,故答案为D
考点:数列求和
点评:主要是考查了数列的周期性的运用,来求解数列的和,属于基础题。

练习册系列答案
相关题目
等比数列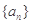 的前
的前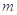 项和为4,前
项和为4,前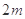 项和为12,则它的前
项和为12,则它的前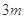 项和是
项和是
| A.28 | B.48 | C.36 | D.52 |
已知等差数列 满足
满足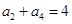 ,
, 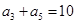 ,则它的前10项和
,则它的前10项和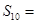 ( )
( )
| A.85 | B.135 | C.95 | D.23 |
已知数列 的前
的前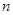 项和为
项和为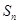 ,若点
,若点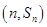
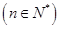 在函数
在函数 的图像上,则
的图像上,则 的通项公式是( )
的通项公式是( )
A.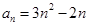 | B.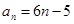 |
C.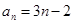 | D.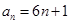 |
数列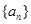 的前n项和为
的前n项和为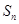 ,若
,若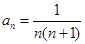 ,则
,则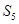 等于( )
等于( )
| A.1 | B. | C.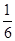 | D.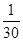 |
已知数列 的前
的前 项和
项和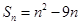 ,第
,第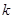 项满足
项满足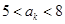 ,则k=( )
,则k=( )
| A.9 | B.8 | C.7 | D.6 |
已知数列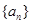 满足:
满足: ,定义使
,定义使 为整数的
为整数的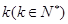 叫做希望数,则区间[1,2013] 内所有希望数的和M=( )
叫做希望数,则区间[1,2013] 内所有希望数的和M=( )
| A.2026 | B.2036 | C.32046 | D.2048 |
等差数列{an}中,若a1+a4+a7=39,a3+a6+a9=27,则前9项的和S9等于( ).
| A.66 | B.99 |
| C.144 | D.297 |
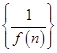 n∈(N*)的前n项和( )
n∈(N*)的前n项和( )