题目内容
若数列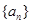 与
与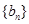 满足
满足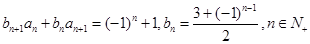 ,且
,且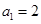 ,设数列
,设数列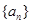 的前
的前 项和为
项和为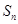 ,则
,则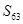 =.
=.
560
解析试题分析:由已知得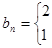
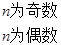 ,
,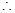 当
当 为奇数时,
为奇数时,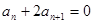 ①,当
①,当 为偶数时,
为偶数时,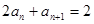 ②,由②得:当
②,由②得:当 为奇数时,
为奇数时,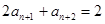 ,结合①式,
,结合①式,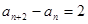 ,所以奇数项为公差为2的等差数列,由①得:
,所以奇数项为公差为2的等差数列,由①得: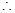 当
当 为奇数时,
为奇数时,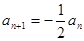 ,所以偶数项为公差为-1的等差数列,
,所以偶数项为公差为-1的等差数列,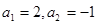 ,所以钱63项有31项偶数,32项奇数,所以
,所以钱63项有31项偶数,32项奇数,所以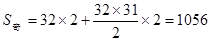 ,
,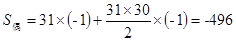 ,
,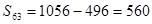 .
.
考点:1.数列的递推公式;2.数列的求和.

练习册系列答案
相关题目
已知数列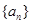 满足:
满足: ,定义使
,定义使 为整数的
为整数的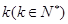 叫做希望数,则区间[1,2013] 内所有希望数的和M=( )
叫做希望数,则区间[1,2013] 内所有希望数的和M=( )
| A.2026 | B.2036 | C.32046 | D.2048 |
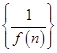 n∈(N*)的前n项和( )
n∈(N*)的前n项和( )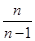
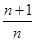
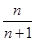

 ,2
,2 ,3
,3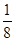 ,4
,4 ,…的前n项和为 .
,…的前n项和为 .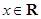 ,函数
,函数 满足
满足 ,设
,设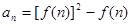 ,数列
,数列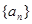 的前15项的和为
的前15项的和为 ,则
,则 .
. ,规定
,规定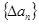 为数列
为数列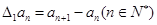 .对于正整数
.对于正整数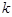 ,规定
,规定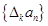 为
为 .若数列
.若数列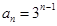 ,则
,则 .
.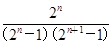 ,则其前n项和Sn=________.
,则其前n项和Sn=________.