题目内容
已知椭圆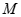 的对称轴为坐标轴,焦点是
的对称轴为坐标轴,焦点是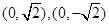 ,又点
,又点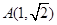 在椭圆
在椭圆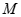 上.
上.
(1)求椭圆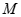 的方程;
的方程;
(2)已知直线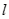 的斜率为
的斜率为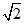 ,若直线
,若直线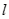 与椭圆
与椭圆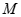 交于
交于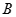 、
、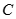 两点,求
两点,求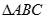 面积的最大值.
面积的最大值.
(1)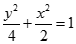 ;(2)
;(2)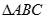 面积的最大值为
面积的最大值为 .
.
解析试题分析:(1)根据椭圆的焦点可设椭圆的方程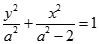 ,然后将
,然后将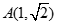 代入可求解得
代入可求解得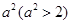 ,从而可确定椭圆的方程;(2)设直线
,从而可确定椭圆的方程;(2)设直线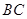 的方程
的方程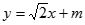 及
及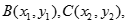 ,联立直线与椭圆的方程,消去
,联立直线与椭圆的方程,消去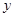 得到
得到 ,先由
,先由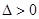 确定
确定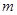 的取值范围,然后根据二次方程根与系数的关系得到
的取值范围,然后根据二次方程根与系数的关系得到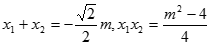 ,从而由公式
,从而由公式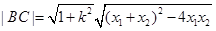 计算出
计算出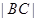 ,再由点到直线的距离公式计算出点
,再由点到直线的距离公式计算出点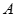 到
到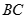 的距离为
的距离为 ,最后得到
,最后得到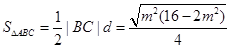 ,利用基本不等式可得面积的最大值.
,利用基本不等式可得面积的最大值.
试题解析:(1)由已知椭圆的焦点为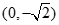 ,故设椭圆方程为
,故设椭圆方程为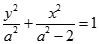 2分
2分
将点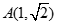 代入方程得
代入方程得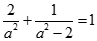 ,整理得
,整理得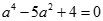 4分
4分
解得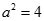 或
或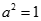 (舍),故所求椭圆方程为
(舍),故所求椭圆方程为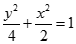 6分
6分
(2)设直线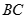 的方程为
的方程为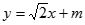 ,设
,设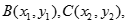 7分
7分
代入椭圆方程并化简得 9分
9分
由 ,可得
,可得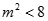 ①
①
由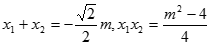 11分
11分
故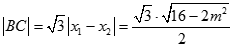
又点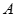 到
到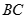 的距离为
的距离为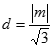 13分
13分
故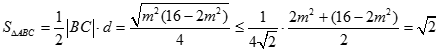
当且仅当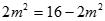 ,即
,即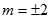 时取等号(满足①式)
时取等号(满足①式)
所以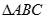 面积的最大值为
面积的最大值为 15分.
15分.
考点:1.椭圆的标准方程;2.直线与圆锥曲线的综合问题;3.基本不等式.

练习册系列答案
相关题目
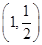 到抛物线C:y2=2px(p>0)的准线的距离为
到抛物线C:y2=2px(p>0)的准线的距离为 .点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB被直线OM平分.
.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB被直线OM平分.
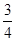 .
. .过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).
.过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).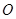 的抛物线
的抛物线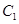 的焦点
的焦点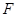 与椭圆
与椭圆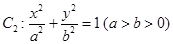 的右焦点重合
的右焦点重合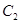 在第一和第四象限的交点分别为
在第一和第四象限的交点分别为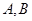 .
.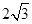 的正三角形,求抛物线
的正三角形,求抛物线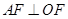 ,求椭圆
,求椭圆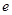 ;
; 为椭圆
为椭圆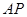 、
、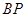 分别与
分别与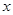 轴交于点
轴交于点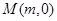 和
和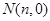 ,证明:
,证明: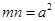 .
. +
+ =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为 .
. 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标. 的焦点为椭圆
的焦点为椭圆 的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.
的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.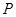 满足:
满足: ,直线
,直线 与
与 的斜率之积为
的斜率之积为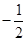 ,证明:存在定点
,证明:存在定点 使
使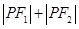 为定值,并求出
为定值,并求出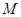 在第一象限,且点
在第一象限,且点 关于原点对称,
关于原点对称, 垂直于
垂直于 轴于点
轴于点 ,连接
,连接 并延长交椭圆于点
并延长交椭圆于点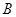 ,记直线
,记直线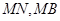 的斜率分别为
的斜率分别为 ,证明:
,证明: .
.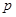 :方程
:方程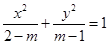 表示的曲线是焦点在y轴上的双曲线,命题
表示的曲线是焦点在y轴上的双曲线,命题 :方程
:方程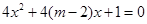 无实根,若
无实根,若 为真,求实数
为真,求实数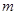 的取值范围.
的取值范围.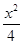 +y2=1上的三个点,O是坐标原点.
+y2=1上的三个点,O是坐标原点.