题目内容
如图所示,在直角坐标系xOy中,点P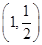 到抛物线C:y2=2px(p>0)的准线的距离为
到抛物线C:y2=2px(p>0)的准线的距离为 .点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB被直线OM平分.
.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB被直线OM平分.
(1)求p,t的值;
(2)求△ABP面积的最大值.
(1) 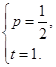 (2)
(2) 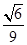
解析解:(1)由题意知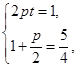 得
得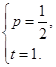
(2)由(1)知M(1,1),
直线OM的方程为y=x,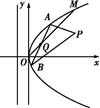
设A(x1,y1),B(x2,y2),线段AB的中点为Q(m,m).
由题意知,
设直线AB的斜率为k(k≠0).
由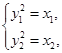
得(y1-y2)(y1+y2)=x1-x2,
故k·2m=1,
所以直线AB的方程为y-m=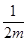 (x-m),
(x-m),
即x-2my+2m2-m=0.
由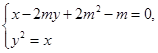 消去x,
消去x,
整理得y2-2my+2m2-m=0,
所以Δ=4m-4m2>0,
y1+y2=2m,y1y2=2m2-m.
从而|AB|= ·|y1-y2|=
·|y1-y2|=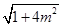 ·
·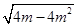 .
.
设点P到直线AB的距离为d,
则d=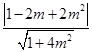 .
.
设△ABP的面积为S,则
S= |AB|·d=|1-2(m-m2)|·
|AB|·d=|1-2(m-m2)|·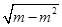 .
.
由Δ=4m-4m2>0,得0<m<1.
令u=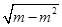 ,0<u≤
,0<u≤ ,则S=u(1-2u2).
,则S=u(1-2u2).
设S(u)=u(1-2u2),0<u≤ ,则S′(u)=1-6u2.
,则S′(u)=1-6u2.
由S′(u)=0,得u=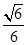 ∈
∈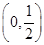 ,
,
因此S(u)在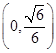 单调递增,在
单调递增,在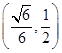 单调递减,
单调递减,
所以S(u)max=S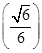 =
=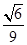 .
.
故△ABP面积的最大值为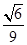 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
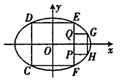
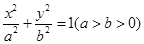 ,且它的四条边与坐标轴平行,正方形GHPQ的顶点G,H在椭圆上,顶点P,Q在正方形的边EF上.且CD=2PQ=
,且它的四条边与坐标轴平行,正方形GHPQ的顶点G,H在椭圆上,顶点P,Q在正方形的边EF上.且CD=2PQ=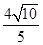 .
.
 +
+ =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.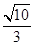 时,求k的值.
时,求k的值.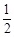 ),延长PB与曲线E交于另一点Q,如果存在某一位置,使得从PQ的中点R向l作垂线,垂足为C,满足PC⊥QC,求a的取值范围。
),延长PB与曲线E交于另一点Q,如果存在某一位置,使得从PQ的中点R向l作垂线,垂足为C,满足PC⊥QC,求a的取值范围。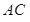 、
、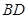 是过抛物线
是过抛物线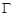 焦点
焦点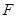 的两条弦,且其焦点
的两条弦,且其焦点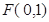 ,
,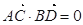 ,点
,点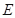 为
为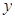 轴上一点,记
轴上一点,记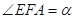 ,其中
,其中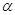 为锐角.
为锐角.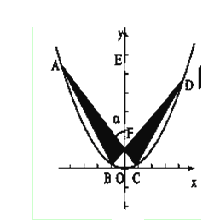
 +y2=1(a>1)的上顶点为A,离心率为
+y2=1(a>1)的上顶点为A,离心率为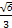 ,若不过点A的动直线l与椭圆C相交于P,Q两点,且
,若不过点A的动直线l与椭圆C相交于P,Q两点,且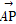 ·
·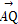 =0.
=0.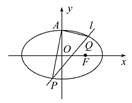
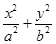 =1(a>b>0)的右焦点为F,过原点和x轴不重合的直线与椭圆E相交于A,B两点,且|AF|+|BF|=2
=1(a>b>0)的右焦点为F,过原点和x轴不重合的直线与椭圆E相交于A,B两点,且|AF|+|BF|=2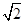 ,|AB|的最小值为2.
,|AB|的最小值为2.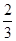 的切线L与椭圆E相交于P,Q两点,当P,Q两点横坐标不相等时,OP(O为坐标原点)与OQ是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
的切线L与椭圆E相交于P,Q两点,当P,Q两点横坐标不相等时,OP(O为坐标原点)与OQ是否垂直?若垂直,请给出证明;若不垂直,请说明理由.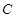 :
: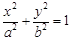 (
(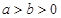 )的焦距为
)的焦距为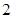 ,且过点(
,且过点(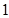 ,
,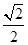 ),右焦点为
),右焦点为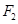 .设
.设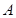 ,
,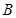 是
是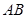 的中点
的中点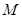 的横坐标为
的横坐标为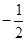 ,线段
,线段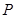 ,
,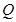 两点.
两点.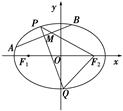
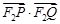 的取值范围.
的取值范围.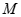 的对称轴为坐标轴,焦点是
的对称轴为坐标轴,焦点是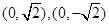 ,又点
,又点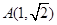 在椭圆
在椭圆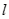 的斜率为
的斜率为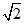 ,若直线
,若直线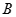 、
、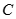 两点,求
两点,求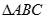 面积的最大值.
面积的最大值.