题目内容
已知顶点为原点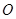 的抛物线
的抛物线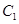 的焦点
的焦点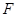 与椭圆
与椭圆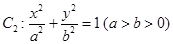 的右焦点重合
的右焦点重合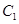 与
与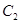 在第一和第四象限的交点分别为
在第一和第四象限的交点分别为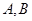 .
.
(1)若△AOB是边长为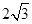 的正三角形,求抛物线
的正三角形,求抛物线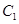 的方程;
的方程;
(2)若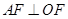 ,求椭圆
,求椭圆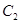 的离心率
的离心率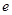 ;
;
(3)点 为椭圆
为椭圆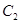 上的任一点,若直线
上的任一点,若直线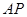 、
、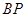 分别与
分别与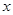 轴交于点
轴交于点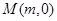 和
和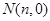 ,证明:
,证明: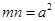 .
.
(1)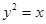 ;(2)
;(2)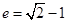 ;(3)证明过程详见试题解析.
;(3)证明过程详见试题解析.
解析试题分析:(1)由△AOB是边长为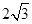 的正三角形得到
的正三角形得到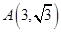 ,代入抛物线方程
,代入抛物线方程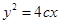 中,可以得到所求抛物线方程为
中,可以得到所求抛物线方程为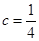 ;(2)由
;(2)由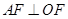 可知点
可知点 的横坐标是
的横坐标是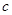 ,因此可结合
,因此可结合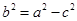 建立关于
建立关于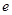 的方程为:
的方程为: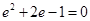 ,解出
,解出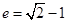 ;(3)利用设而不求的思想,可先设
;(3)利用设而不求的思想,可先设 三点后代入椭圆方程中,由于
三点后代入椭圆方程中,由于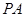 的方程为
的方程为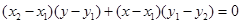 ,求出
,求出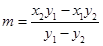 ,
,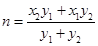 ,那么
,那么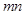 化简后得到:
化简后得到: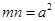 .
.
试题解析:(1)设椭圆的右焦点为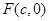 ,依题意得抛物线的方程为
,依题意得抛物线的方程为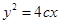
∵△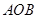 是边长为
是边长为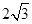 的正三角形,
的正三角形,
∴点A的坐标是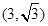 ,
,
代入抛物线的方程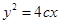 解得
解得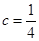 ,
,
故所求抛物线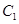 的方程为
的方程为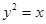
(2)∵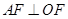 , ∴ 点
, ∴ 点 的横坐标是
的横坐标是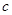
代入椭圆方程解得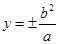 ,即点
,即点 的坐标是
的坐标是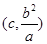
∵ 点 在抛物线
在抛物线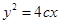 上,
上,
∴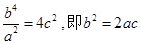 ,
,
将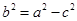 代入上式整理得:
代入上式整理得: ,
,
即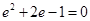 ,解得
,解得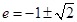
∵ 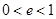 ,故所求椭圆
,故所求椭圆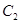 的离心率
的离心率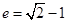 .
.
(3)证明:设 ,代入椭圆方程得
,代入椭圆方程得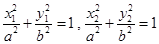
而直线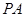 的方程为
的方程为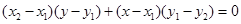
令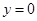 得
得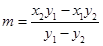 .
.
在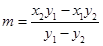 中,以
中,以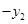 代换
代换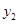 得
得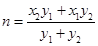
∴ 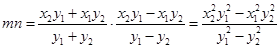
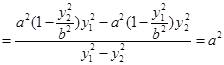 .
.
考点:圆锥曲线;直线与圆锥曲线的位置关系.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
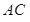 、
、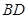 是过抛物线
是过抛物线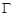 焦点
焦点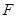 的两条弦,且其焦点
的两条弦,且其焦点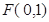 ,
,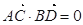 ,点
,点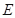 为
为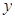 轴上一点,记
轴上一点,记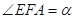 ,其中
,其中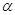 为锐角.
为锐角.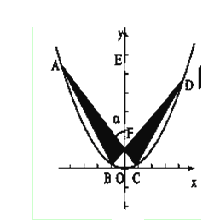
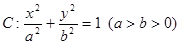 的右焦点为
的右焦点为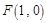 ,设左顶点为A,上顶点为B且
,设左顶点为A,上顶点为B且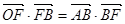 ,如图.
,如图.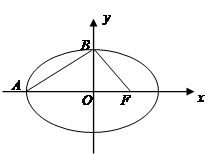
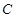 的方程;
的方程;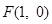 ,过
,过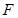 的直线
的直线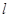 交椭圆于
交椭圆于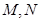 两点,试确定
两点,试确定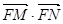 的取值范围.
的取值范围. =1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,点F2(c,0)到直线l:x=
=1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,点F2(c,0)到直线l:x=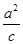 的距离为3.
的距离为3. ⊥
⊥ ,求出该圆的方程.
,求出该圆的方程.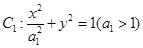 与
与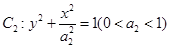 的离心率相等. 直线
的离心率相等. 直线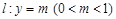 与曲线
与曲线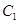 交于
交于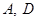 两点(
两点(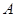 在
在 的左侧),与曲线
的左侧),与曲线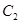 交于
交于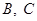 两点(
两点( 在
在 的左侧),
的左侧),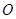 为坐标原点,
为坐标原点,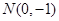 .
.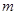 =
=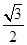 ,
,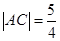 时,求椭圆
时,求椭圆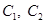 的方程;
的方程;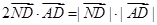 ,且
,且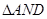 和
和 相似,求
相似,求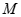 的对称轴为坐标轴,焦点是
的对称轴为坐标轴,焦点是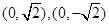 ,又点
,又点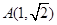 在椭圆
在椭圆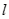 的斜率为
的斜率为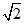 ,若直线
,若直线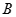 、
、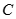 两点,求
两点,求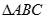 面积的最大值.
面积的最大值. +
+ =1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,
=1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上, ·
·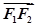 =0,3|
=0,3|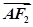 |·|
|·|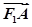 |=-5
|=-5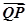 ·
·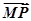 =
=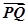 ·
·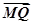 ?若存在,求出实数m的取值范围;若不存在,说明理由.
?若存在,求出实数m的取值范围;若不存在,说明理由.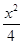 +y2=1上的三个点,O是坐标原点.
+y2=1上的三个点,O是坐标原点.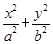 =1(a>b>0)的右焦点为F2(1,0),点A
=1(a>b>0)的右焦点为F2(1,0),点A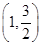 在椭圆上.
在椭圆上.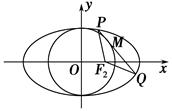
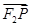 |+|
|+|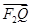 |+|
|+|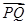 |是否为定值?如果是,求出该定值;如果不是,说明理由.
|是否为定值?如果是,求出该定值;如果不是,说明理由.