题目内容
【题目】已知集合![]() .
.
(1)求证:函数![]() ;
;
(2)某同学由(1)又发现![]() 是周期函数且是偶函数,于是他得出两个命题:①集合
是周期函数且是偶函数,于是他得出两个命题:①集合![]() 中的元素都是周期函数;②集合
中的元素都是周期函数;②集合![]() 中的元素都是偶函数,请对这两个命题给出判断,如果正确,请证明;如果不正确,请举出反例;
中的元素都是偶函数,请对这两个命题给出判断,如果正确,请证明;如果不正确,请举出反例;
(3)设![]() 为非零常数,求
为非零常数,求![]() 的充要条件,并给出证明.
的充要条件,并给出证明.
【答案】(1)见解析(2)命题①正确.见解析(3)充要条件是![]() 或
或![]() ,见解析
,见解析
【解析】
(1)通过计算证明![]() ,即可得证;
,即可得证;
(2)根据函数关系代换![]() ,即可证明周期性,举出反例
,即可证明周期性,举出反例![]() 不是偶函数;
不是偶函数;
(3)根据充分性和必要性分别证明![]() 或
或![]() .
.
(1)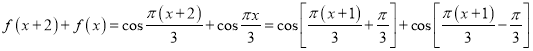
![]()
∴![]()
∴![]()
(2)命题①正确.集合![]() 中的元素都是周期函数.
中的元素都是周期函数.
证明:若![]()
则![]() 可得
可得![]() .
.
所以![]() ,从而
,从而![]() ,
,
所以![]() 为周期函数,命题①正确;命题②不正确.
为周期函数,命题①正确;命题②不正确.
如![]() 不是偶函数,但满足
不是偶函数,但满足![]() ,这是因为
,这是因为
![]()
![]()
∴![]()
∴![]()
(3)若![]()
则![]() ,
,![]()
∴![]()
∴![]()
∴![]() ,可得∴
,可得∴![]()
∴![]() 或
或![]()
当![]() 或
或![]() 时
时
![]()
![]()
![]()
∴![]()
所以![]() 的充要条件是
的充要条件是![]() 或
或![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目