题目内容
7.已知cosα-cosβ=-$\frac{1}{2}$,sinα-sinβ=$\frac{1}{4}$,求tanαtanβ.分析 条件平方,化简可得2cosαcosβ=$\frac{3}{4}$,2sinαsinβ=$\frac{15}{16}$,利用tanαtanβ=$\frac{sinαsinβ}{cosαcosβ}$,可得结论.
解答 解:两式分别平方可得1-2cosαcosβ=$\frac{1}{4}$,1-2sinαsinβ=$\frac{1}{16}$,
∴2cosαcosβ=$\frac{3}{4}$,2sinαsinβ=$\frac{15}{16}$,
∴tanαtanβ=$\frac{sinαsinβ}{cosαcosβ}$=$\frac{5}{4}$.
点评 本题考查同角三角函数关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
18.设log89=a,log35=b,则lg2=( )
| A. | $\frac{2}{2+3ab}$ | B. | $\frac{1-a}{2ab}$ | C. | $\frac{1-a}{a+2b}$ | D. | $\frac{1-a}{{a}^{2}+b}$ |
15.-700°是( )角.
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.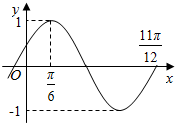 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )
 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
15.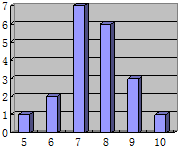 某射击小组有20个人,教练根据他们某次射击的数据绘制成如图的统计图,则这组数据的众数和中位数分别是( )
某射击小组有20个人,教练根据他们某次射击的数据绘制成如图的统计图,则这组数据的众数和中位数分别是( )
 某射击小组有20个人,教练根据他们某次射击的数据绘制成如图的统计图,则这组数据的众数和中位数分别是( )
某射击小组有20个人,教练根据他们某次射击的数据绘制成如图的统计图,则这组数据的众数和中位数分别是( )| A. | 7,7 | B. | 8,7.5 | C. | 7,7.5 | D. | 8,6 |
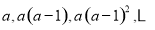 ,其前
,其前 项和为
项和为 .
. 的取值范围及
的取值范围及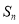 ;
;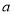 ,使
,使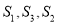 成等差数列?若存在,求出
成等差数列?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由. 中,角
中,角 所对的边分别为
所对的边分别为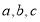 .若
.若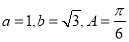 ,则角
,则角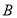 等于( )
等于( )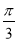 B.
B.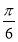 C.
C.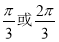 D.
D.