题目内容
10.从5名男生医生、2名女医生中选3名医生组成一个医疗小分队,要求其中至少有1名女医生,则不同的组队方案共有( )| A. | 30种 | B. | 25种 | C. | 20种 | D. | 10种 |
分析 这3人中至少有1名女医生与只选男医生为对立事件,则这3人中至少有1名女医生等于从全部方案中减去只选男医生的方案数,由排列的方法计算全部方案与只选男医生的方案数
解答 解:5名男生医生、2名女医生中选3名医生组成一个医疗小分队,有C73种选法,
其中只选派男医生的方案数为C53,
这3人中至少有1名女医生与只选男医生为对立事件,
则这3人中至少有1名女医生等于从全部方案中减去只选男医生的方案数,
即合理的选则方案共有C73-C53=25种结果,
故选:B.
点评 本题考查排列组合的运用,本题解题的关键是看出要求的事件的对立事件,遇到求出现至多或至少这种语言时,一般要用间接法来解,正难则反.

练习册系列答案
相关题目
15.变量x、y满足约束条件$\left\{\begin{array}{l}x+2y≥2\\ 2x+y≤4\\ 4x-y≥-1\end{array}\right.$,则目标函数z=3x-y+3的取值范围是( )
| A. | $[\frac{3}{2},9]$ | B. | $[\frac{3}{2},6]$ | C. | [-2,9] | D. | [2,9] |
 ,在0处的导数为27,则
,在0处的导数为27,则 ( )
( ) 如图,在△ABC中,∠C=90°,∠ABC平分线BE交AC于点E,点D在AB上,∠DEB=90°.
如图,在△ABC中,∠C=90°,∠ABC平分线BE交AC于点E,点D在AB上,∠DEB=90°. 定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若函数f(x)=2→x,则f(2)+f(-2)=( )
定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若函数f(x)=2→x,则f(2)+f(-2)=( )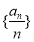 是公差为2的等差数列,且
是公差为2的等差数列,且 ,则数列
,则数列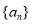 的前
的前 项和
项和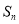 取得最小值时,
取得最小值时,