题目内容
3.已知向量$\overrightarrow{a}$=(sin2x,cosx),$\overrightarrow{b}$=(1,-2cosx),则函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$的最小正周期为π.分析 由条件利用二倍角公式、两角和差正弦公式求得f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$)-1,可得它的最小周期.
解答 解:函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=sin2x-2oos2x=sin2x-2•$\frac{1+cos2x}{2}$=$\sqrt{2}$sin(2x-$\frac{π}{4}$)-1,
故它的最小正周期为$\frac{2π}{2}$=π,
故答案为:π.
点评 本题主要考查两角和差的正弦公式、二倍角公式,正弦函数的周期性,属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
18.下列函数中,既是奇函数又在区间(0,+∞)上单调递增的函数是( )
| A. | y=lnx | B. | y=x3 | C. | $y={(\frac{1}{2})^x}$ | D. | y=sinx |
8.下列说法中,正确的是( )
| A. | 命题“若am2<bm2,则a<b”的逆命题是真命题 | |
| B. | 命题“存在x∈R,2x>0,”的否定是:“任意x∈R,2x≤0” | |
| C. | 命题p或q为真命题,则命题p和命题q均为真命题 | |
| D. | 命题p且q为真命题,则命题p和q命题至少有一个是真命题 |
10.从5名男生医生、2名女医生中选3名医生组成一个医疗小分队,要求其中至少有1名女医生,则不同的组队方案共有( )
| A. | 30种 | B. | 25种 | C. | 20种 | D. | 10种 |
 中,
中, ,
,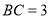 ,
, ,
, 是
是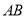 上的点,则
上的点,则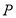 到
到 的距离的乘积的最大值为( )
的距离的乘积的最大值为( ) D.9
D.9