题目内容
19.当a为何值时,不等式(a2-1)x2-(a-1)x-1<0的解集为R.分析 讨论a2-1=0时和a2-1≠0时,不等式解集的情况,从而求出满足题意的a的取值范围
解答 解:当a2-1=0时,a=±1,
若a=1,不等式化为-1<0,满足题意,
若a=-1,不等式化为2x-1<0,不满足题意;
当1-a2≠0时,即a≠±1,
∴$\left\{\begin{array}{l}{{a}^{2}-1<0}\\{(a-1)^{2}+4({a}^{2}-1)<0}\end{array}\right.$,
即;$\left\{\begin{array}{l}{-1<a<1}\\{-\frac{3}{5}<a<1}\end{array}\right.$
解得-$\frac{3}{5}$<a<1;
综上,a的取值范围(-$\frac{3}{5}$,1].
点评 本题考查了不等式恒成立的问题,解题时应对字母系数进行讨论,是基础题

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
10.从5名男生医生、2名女医生中选3名医生组成一个医疗小分队,要求其中至少有1名女医生,则不同的组队方案共有( )
| A. | 30种 | B. | 25种 | C. | 20种 | D. | 10种 |
某市乘坐出租车的收费办法如下:
⑴不超过4千米的里程收费12元; ⑵超过4千米的里程按每千米2元收费(对于其中不足千米的部分,若其小于0.5千米则不收费,若其大于或等于0.5千米则按1千米收费); 当车程超过4千米时,另收燃油附加费1元. |
相应系统收费的程序框图如图所示,其中 (单位:千米)为行驶里程,
(单位:千米)为行驶里程, (单位:元)为所收费用,用
(单位:元)为所收费用,用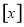 表示不大于
表示不大于 的最大整数,则图中①处应填( )
的最大整数,则图中①处应填( )

A.  B.
B.  C.
C.  D.
D. 
 中,曲线
中,曲线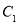 的参数方程为
的参数方程为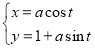 (
( 为参数,
为参数,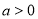 ),在以坐标原点为极点,
),在以坐标原点为极点, 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 .
.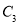 的极坐标方程为
的极坐标方程为 ,其中
,其中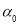 满足
满足 ,若曲线
,若曲线 的公共点都在
的公共点都在 上,求
上,求 .
. ,在0处的导数为27,则
,在0处的导数为27,则 ( )
( )