题目内容
求下列双曲线的标准方程.(1)与椭圆
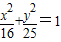 共焦点,且过点
共焦点,且过点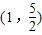 的双曲线;
的双曲线;(2)与双曲线
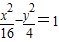 有相同渐近线,且过点
有相同渐近线,且过点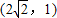 的双曲线.
的双曲线.
【答案】分析:(1)根据双曲线的焦点与椭圆的焦点相同可求出c的值,设出双曲线方程,将点代入可求出所求;
(2)与双曲线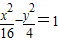 有相同渐近线的双曲线方程可设为
有相同渐近线的双曲线方程可设为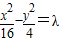 ,将点代入可求出λ的值,从而可求出所求.
,将点代入可求出λ的值,从而可求出所求.
解答:解:(1)椭圆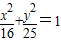 焦点坐标为(0,3),在y轴上
焦点坐标为(0,3),在y轴上
∴所求双曲线的焦点坐标为(0,3),c=3
故设双曲线方程为
∵点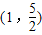 在双曲线上
在双曲线上
∴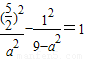 解得a2=5,
解得a2=5,
∴所求双曲线方程为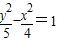
(2)与双曲线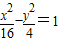 有相同渐近线的双曲线方程可设为
有相同渐近线的双曲线方程可设为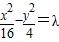
而点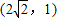 在双曲线上则
在双曲线上则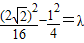 解得λ=
解得λ=
∴所求双曲线方程为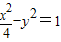
点评:本题主要考查了椭圆、双曲线的标准方程,以及圆锥曲线的性质,同时考查了运算求解的能力,属于中档题.
(2)与双曲线
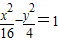 有相同渐近线的双曲线方程可设为
有相同渐近线的双曲线方程可设为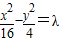 ,将点代入可求出λ的值,从而可求出所求.
,将点代入可求出λ的值,从而可求出所求.解答:解:(1)椭圆
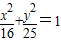 焦点坐标为(0,3),在y轴上
焦点坐标为(0,3),在y轴上∴所求双曲线的焦点坐标为(0,3),c=3
故设双曲线方程为

∵点
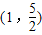 在双曲线上
在双曲线上∴
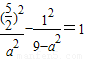 解得a2=5,
解得a2=5,∴所求双曲线方程为
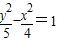
(2)与双曲线
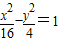 有相同渐近线的双曲线方程可设为
有相同渐近线的双曲线方程可设为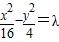
而点
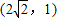 在双曲线上则
在双曲线上则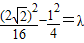 解得λ=
解得λ=
∴所求双曲线方程为
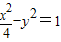
点评:本题主要考查了椭圆、双曲线的标准方程,以及圆锥曲线的性质,同时考查了运算求解的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
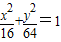 有相同的焦点,且离心率为
有相同的焦点,且离心率为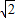 .
.