题目内容
求下列双曲线的标准方程:(1)过点(3,-1),渐近线方程是y=±3x;
(2)与椭圆
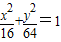 有相同的焦点,且离心率为
有相同的焦点,且离心率为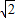 .
.
【答案】分析:(1)根据题意,双曲线的渐近线方程是y=±3x,可设双曲线方程为 9x2-y2=λ(λ≠0),又由双曲线过点(3,-1),将点P的坐标代入可得λ的值,进而可得答案.
(2)由椭圆的性质,可得椭圆 的焦点坐标,由双曲线的离心率可设双曲线方程为为 y2-x2=a2(a>0),则可得a的值,进而可得双曲线方程.
的焦点坐标,由双曲线的离心率可设双曲线方程为为 y2-x2=a2(a>0),则可得a的值,进而可得双曲线方程.
解答:解:根据题意,双曲线的渐近线方程是y=±3x,
设双曲线方程为 9x2-y2=λ(λ≠0),
∵双曲线过点(3,-1),
∴9×9-1=λ,即λ=80.
∴所求双曲线方程为 ;
;
(2)∵椭圆 的焦点坐标为(0,4
的焦点坐标为(0,4 )和(0,-4
)和(0,-4 ),
),
根据双曲线的离心率为 .则可设双曲线方程为 y2-x2=a2(a>0),
.则可设双曲线方程为 y2-x2=a2(a>0),
∵c=4 ,即
,即  =4
=4 ,
,
∴a=2 .
.
故所求双曲线方程为 .
.
点评:本题考查双曲线的标准方程的求法,考查双曲线的标准方程以及椭圆的简单几何性质,注意区分并记忆椭圆、双曲线的几何性质及标准方程的形式.
(2)由椭圆的性质,可得椭圆
 的焦点坐标,由双曲线的离心率可设双曲线方程为为 y2-x2=a2(a>0),则可得a的值,进而可得双曲线方程.
的焦点坐标,由双曲线的离心率可设双曲线方程为为 y2-x2=a2(a>0),则可得a的值,进而可得双曲线方程.解答:解:根据题意,双曲线的渐近线方程是y=±3x,
设双曲线方程为 9x2-y2=λ(λ≠0),
∵双曲线过点(3,-1),
∴9×9-1=λ,即λ=80.
∴所求双曲线方程为
 ;
;(2)∵椭圆
 的焦点坐标为(0,4
的焦点坐标为(0,4 )和(0,-4
)和(0,-4 ),
),根据双曲线的离心率为
 .则可设双曲线方程为 y2-x2=a2(a>0),
.则可设双曲线方程为 y2-x2=a2(a>0),∵c=4
 ,即
,即  =4
=4 ,
,∴a=2
 .
.故所求双曲线方程为
 .
.点评:本题考查双曲线的标准方程的求法,考查双曲线的标准方程以及椭圆的简单几何性质,注意区分并记忆椭圆、双曲线的几何性质及标准方程的形式.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
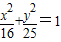 共焦点,且过点
共焦点,且过点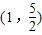 的双曲线;
的双曲线;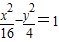 有相同渐近线,且过点
有相同渐近线,且过点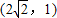 的双曲线.
的双曲线.