题目内容
已知数列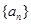 的前
的前 项和
项和 。
。
(1)求数列的通项公式;
(2)求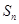 的最大或最小值.
的最大或最小值.
(1) 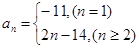 (2)
(2) 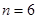 或
或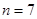 ,此时
,此时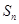 有最小值
有最小值 ,无最大值.
,无最大值.
解析试题分析:(1) 根据已知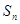 求
求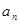 ,可知利用
,可知利用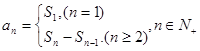 ,求出
,求出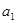 和
和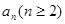 ,而后验证是否可以合为一个通项公式.
,而后验证是否可以合为一个通项公式.
(2)根据 可知,其是一个开口向上的二次函数,其中
可知,其是一个开口向上的二次函数,其中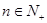 .所以其无最大值,有最小值在对称轴处取得,即
.所以其无最大值,有最小值在对称轴处取得,即 时.但是显然
时.但是显然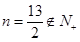 ,所以取离它最近的整数
,所以取离它最近的整数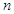 的值,从而得到
的值,从而得到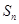 的最小值.
的最小值.
(1)当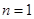 时,
时, ,
,
当 时,
时,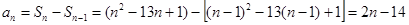 ,
,
验证将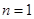 带入
带入 时的
时的 中可得
中可得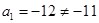 ,不成立,
,不成立,
所以数列的通项公式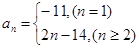 .
.
(2)根据 可知,其是一个开口向上的二次函数,其中
可知,其是一个开口向上的二次函数,其中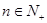 .
.
所以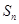 无最大值,有最小值在对称轴处取得,即
无最大值,有最小值在对称轴处取得,即 时,
时,
显然此时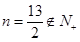 ,所以取离它最近的正整数
,所以取离它最近的正整数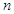 的值,
的值,
即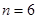 或
或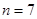 ,此时
,此时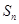 有最小值
有最小值 .
.
考点:已知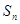 求
求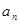 ,可知利用
,可知利用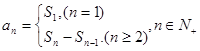 ;将数列前
;将数列前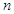 项和当做二次函数求最值.
项和当做二次函数求最值.

练习册系列答案
相关题目
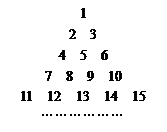
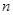 行(
行(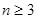 )从左向右的第3个数为 .
)从左向右的第3个数为 . 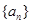 的公差为
的公差为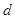 ,点
,点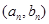 在函数
在函数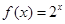 的图象上(
的图象上(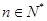 ).
).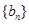 是等比数列;
是等比数列;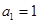 ,学科网函数
,学科网函数 的图象在点
的图象在点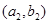 处的切线在
处的切线在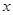 轴上的截距为
轴上的截距为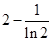 ,求数列
,求数列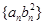 的前
的前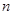 项和
项和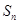 .
.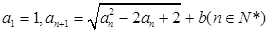
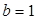 ,求
,求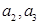 及数列
及数列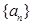 的通项公式;
的通项公式;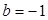 ,问:是否存在实数
,问:是否存在实数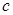 使得
使得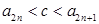 对所有
对所有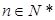 成立?证明你的结论.
成立?证明你的结论.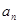 }满足
}满足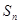 +
+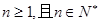 )
)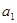 ,
,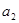 ,
,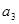 的值;
的值;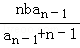 (n≥2)
(n≥2)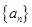 ,
,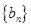 满足
满足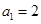 ,
,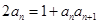 ,
,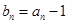 ,数列
,数列 项和为
项和为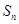 ,
,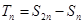 .
.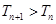 ;
;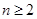 时,
时,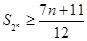 .
.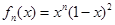 在
在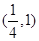 上的最大值为
上的最大值为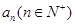
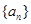 的通项公式;
的通项公式;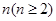 ,都有
,都有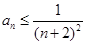 ;
;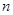 项和
项和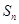 ,求证:对任何正整数
,求证:对任何正整数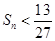 成立
成立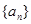 满足:
满足: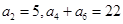 ,
,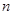 项和为
项和为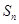 .
.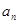 及
及 ,求数列
,求数列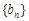 的前
的前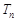 .
.