题目内容
8．设点P在直线y=x上，点Q在曲线y=lnx上，则|PQ|最小值为（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | $\sqrt{2}$ | C． | $\sqrt{2}$-1 | D． | ln2 |
分析 设平行于直线y=x的直线y=x+b与曲线y=lnx相切，则两平行线间的距离即为|PQ|的最小值，由导数和切线的关系由距离公式可得．
解答 解：设平行于直线y=x的直线y=x+b与曲线y=lnx相切，
则两平行线间的距离即为|PQ|的最小值，
设直线y=x+b与曲线y=lnx的切点为（m，lnm），
则由切点还在直线y=x+b可得lnm=m+b，
由切线斜率等于切点的导数值可得$\frac{1}{m}$=1，
联立解得m=1，b=-1，
∴由平行线间的距离公式可得|PQ|的最小值为$\frac{|-1-0|}{\sqrt{{1}^{2}+（-1）^{2}}}$=$\frac{\sqrt{2}}{2}$
故选：A．
点评 本题考查导数和平行线间的距离公式，等价转化是解决问题的关键，属基础题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
18．
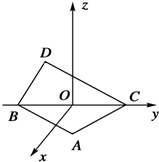如图所示，在空间直角坐标系中BC=2，原点O是BC的中点，点A的坐标是（$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$，0），点D在平面yOz上，且∠BDC=90°，∠DCB=30°，则向量$\overrightarrow{AD}$的坐标为（ ）
如图所示，在空间直角坐标系中BC=2，原点O是BC的中点，点A的坐标是（$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$，0），点D在平面yOz上，且∠BDC=90°，∠DCB=30°，则向量$\overrightarrow{AD}$的坐标为（ ）| A． | （-$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$） | B． | （-$\frac{\sqrt{3}}{2}$，-1，$\frac{\sqrt{3}}{2}$） | C． | （-$\frac{1}{2}$，-$\frac{\sqrt{3}}{2}$，$\frac{\sqrt{3}}{2}$） | D． | （$\frac{\sqrt{3}}{2}$，1，$\frac{\sqrt{3}}{2}$） |
19．若曲线f（x）=sinx-$\sqrt{2}$cosx的切线的倾斜角为α，则α的取值范围为（ ）
| A． | $[0，\frac{π}{3}]$ | B． | $[\frac{π}{3}，\frac{2}{3}π]$ | C． | $[0，\frac{π}{3}]∪[\frac{2}{3}π，π）$ | D． | $[0，\frac{π}{3}]∪[\frac{2}{3}π，π]$ |
3．$\int\begin{array}{l}1\\ 0\end{array}\;x\;dx$=（ ）
| A． | -1 | B． | 0 | C． | $\frac{1}{2}$ | D． | 1 |
20．已知点A（-3，0）、B（3，0），动点P满足||PA|-|PB||=m，则0＜m＜6是动点P的轨迹为双曲线的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |