题目内容
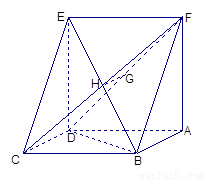
（本题满分14分）已知如图：平行四边形ABCD中，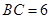
，正方形ADEF所在平面与平面ABCD垂直，G，H分别是DF，BE的中点．
（１）求证：GH∥平面CDE；
（２）若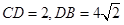
，求四棱锥F-ABCD的体积．
（1）证法１：∵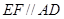
,
∴
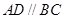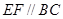且
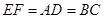
∴四边形EFBC是平行四边形 ∴H为FC的中点-------------2分
又∵G是FD的中点
∴
---------------------------------------4分
∵
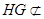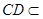平面CDE，
平面CDE
∴GH∥平面CDE -------------------------------------7分
证法２：连结EA，∵ADEF是正方形 ∴G是AE的中点 --------------1分
∴在⊿EAB中，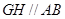
----------------------------------3分
又∵AB∥CD，∴GH∥CD，----------------------------------4分
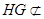∵平面CDE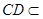，平面CDE
∴GH∥平面CDE ---------------------------------------------7分
（2）∵平面ADEF⊥平面ABCD，交线为AD
且FA⊥AD， ∴FA⊥平面ABCD.---------------------------------------------------9分
∵
, ∴
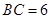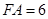又∵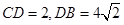
，
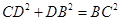
∴BD⊥CD ----------------------------------------------------------------------------------------11分
∴ 
＝
∴ 
＝
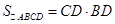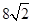
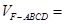
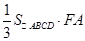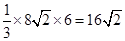-----------------------------------------14分
【解析】略
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
，
，函数
. （Ⅰ）求
的单调增区间； （II）若在
中，角
所对的边分别是
，且满足：
，求
的取值范围.
，且以下命题都为真命题：
实系数一元二次方程
的两根都是虚数；
存在复数
同时满足
且
.
的取值范围.
，求x的值；
对于
恒成立，求实数m的取值范围. 
：
的离心率为
，过坐标原点
且斜率为
的直线
与
、
，
．
、
的值；
与椭圆
的取值范围．
，AB=BC=2AD=4，E、F分别是AB、CD上的点，EF∥BC，AE = x，G是BC的中点．沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF
（如图）.
，
