题目内容
若不等式x+|x-a|＞1的解集为R，则实数a的取值范围是（ ）
分析：画出数轴，对a与1比较分类讨论，通过不等式x+|x-a|＞1的解集为R，求出a的范围．
解答：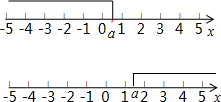
解：画出数轴，当a＜1时，不等式x+|x-a|＞1的解集为R，不成立；
当a=1时，0≤x≤1时，不等式不成立；
当a＞1时，不等式x+|x-a|＞1的解集为R，恒成立；
综上实数a的取值范围是：（1，+∞）．
故选A．
解：画出数轴，当a＜1时，不等式x+|x-a|＞1的解集为R，不成立；当a=1时，0≤x≤1时，不等式不成立；
当a＞1时，不等式x+|x-a|＞1的解集为R，恒成立；
综上实数a的取值范围是：（1，+∞）．
故选A．
点评：本题是中档题，考查绝对值不等式的求法，注意数轴的应用，考查计算能力，逻辑推理能力．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
，x∈A,试判断g(x)的单调性(写明理由，不必证明)；
＞2x+a–5}，且对于(1)中的A，A∩B≠F，求实数a的取值范围。