题目内容
已知数列{an}中,a1=1,且an=
an-1+2n•3n-2(n≥2,n∈N*).
(1)求a2,a3,a4的值;
(2)写出数列{an}的通项公式,并用数学归纳法证明.
| n |
| n-1 |
(1)求a2,a3,a4的值;
(2)写出数列{an}的通项公式,并用数学归纳法证明.
(1)a1=1,且an=
an-1+2n•3n-2(n≥2,n∈N*),
当n=2时,a2=6,n=3时,a3=27,n=4时,a4=108…(3分)
(2)猜想:an=n•3n-1…(5分)
证明:(1)当n=1时,显然成立;…(6分)
(2)假设当n=k时,结论成立,即ak=k•3k-1,则
当n=k+1时,ak+1=
ak+2(k+1)•3k-1=
k•3k-1+2(k+1)•3k-1
=(k+1)•3k=(k+1)•3(k+1)-1
∴当n=k+1时结论也成立.…(10分)
综上(1)(2)可知,对?n∈N*,an=n•3n-1恒成立.…(12分)
| n |
| n-1 |
当n=2时,a2=6,n=3时,a3=27,n=4时,a4=108…(3分)
(2)猜想:an=n•3n-1…(5分)
证明:(1)当n=1时,显然成立;…(6分)
(2)假设当n=k时,结论成立,即ak=k•3k-1,则
当n=k+1时,ak+1=
| k+1 |
| k |
| k+1 |
| k |
=(k+1)•3k=(k+1)•3(k+1)-1
∴当n=k+1时结论也成立.…(10分)
综上(1)(2)可知,对?n∈N*,an=n•3n-1恒成立.…(12分)

练习册系列答案
相关题目
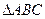 的三个内角
的三个内角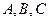 成等差数列,求证:
成等差数列,求证: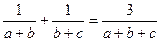
 ,则
,则 .
.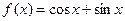 ,问是否存在
,问是否存在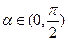 ,
,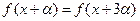 恒成立?证明你的结论.
恒成立?证明你的结论.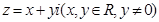 ,
,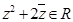 ,
,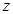 在复平面上所对应点在直线
在复平面上所对应点在直线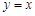 上,则
上,则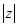 = 。
= 。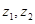 对应的向量分别是
对应的向量分别是 ,则
,则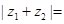 ( )
( )