题目内容
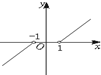
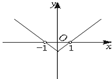
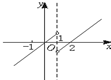
13．下列函数中，在（0，+∞）上是减函数的是（ ）| A． | y=$\sqrt{x}$ | B． | y=lnx | C． | y=$\frac{1}{x}$ | D． | y=2x |
分析 直接利用基本函数的单调性判断即可．
解答 解：y=$\sqrt{x}$在（0，+∞）上是增函数；
y=lnx在（0，+∞）上是增函数；
y=$\frac{1}{x}$在（0，+∞）上是减函数；
y=2x，在（0，+∞）上是增函数；
故选：C．
点评 本题考查基本函数的单调性的应用，考是基础题．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
3．已知ABCD是平行四边形，且A（4，1，3），B（2，-5，1），C（3，7，-5），则顶点D的坐标为（ ）
| A． | （1，1，-7） | B． | （5，13，-3） | C． | （-3，1，5） | D． | （5，3，1） |
4．已知△ABC内角A，B，C的对边分别为a，b，c，且$\frac{a-b}{a-c}$=$\frac{sinC}{sinA+sinB}$，则B=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{3π}{4}$ |
8．若点P（m，3）到直线4x-3y+1=0的距离为5，且点P在不等式2x+y＜3表示的平面区域内，则m=（ ）
| A． | $-\frac{15}{4}$ | B． | $-\frac{17}{4}$ | C． | $\frac{33}{4}$ | D． | $-\frac{17}{4}$或$\frac{33}{4}$ |
如图，在正方形SG1G2G3中，E，F分别是G1G2，G2G3的中点，D是EF的中点，现沿SE，SF及EF把这个正方形折成一个几何体，使G1，G2，G3三点重合于点G，这样，下列五个结论：①SG⊥平面EFG；②SD⊥平面EFG；③GF⊥平面SEF；④EF⊥平面GSD；⑤GD⊥平面SEF．