题目内容
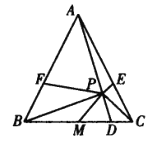
【题目】如图,在△ABC中,AB=AC,M是BC的中点,D、E、F分别是边BC、CA、AB上的点,且AE=AF,△AEF的外接圆交线段AD于点P.若点P满足![]() ,证明:
,证明:![]() .
.
【答案】见解析
【解析】
在△AEF的外接圆中,由于AE=AF,
故![]() .
.
因此,P、D、B、F与P、D、C、E分别四点共圆.
于是,![]() .
.
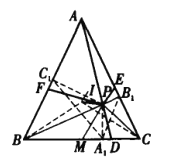
如图,设P在边BC、CA、AB上的射影分别为![]() 、
、![]() 、
、![]() .则△
.则△![]() .
.
由![]() ,得
,得
![]() .①
.①
设△ABC的内心为I,下证:B、I、P、C四点共圆.
联结![]() .因
.因![]() 和
和![]() 分别四点共圆,
分别四点共圆,
则![]() .
.
又由式①,有![]() .
.
所以,![]() .
.
因此,![]() ..
..
而![]() ,
,![]() ,
,
所以,![]()
又![]() ,
,
![]() ,
,![]() .
.
故![]() .
.
因此,B、I、P、C四点共圆.
于是,![]() .
.
如图,延长AM交△ABC的外接圆于点O,则AO为外接圆的直径.于是,OB⊥AB,OC⊥AC,且OB=OI=OC.
因此,点O是点B、I、P、C所在圆的圆心.
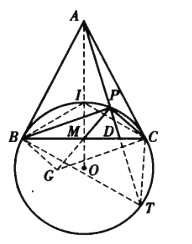
从而,AB、AC为![]() 的切线.
的切线.
延长AD交![]() 于点T,则
于点T,则![]() .
.
所以,![]() .
.
又由![]() ,得
,得![]() .
.
因AB=AC,故
![]() .②
.②
延长PM到点G,使GM=PM,则四边形BPCG为平行四边形有
![]() .③
.③
由式②得![]() .④
.④
由式③、④得![]() .
.
所以,![]() ,即
,即
![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目


