题目内容
在△ABC中,A最大,C最小,且A=2C,a+c=2b,求此三角形的三边之比.
6:5:3
解析试题分析:解:由正弦定理得,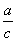 =
=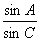 =
=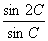 =2cosC,即cosC=
=2cosC,即cosC=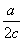 .由余弦定理得cosC=
.由余弦定理得cosC=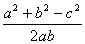 =
=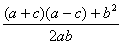 ,
,
∵a+c=2b,
∴cosC=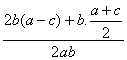 =
=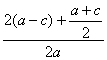 ,
,
∴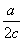 =
=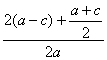 .
.
整理得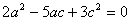 ,故有2a=3c,因此可知5c=4b,故三边之比为6:5:3
,故有2a=3c,因此可知5c=4b,故三边之比为6:5:3
考点:正弦定理和余弦定理
点评:解决的关键是对于两个定理的熟练运用,根据已知的边角关系式化简变形得到求解,属于基础题。

练习册系列答案
相关题目
 ABC中,
ABC中, 所对边分别为
所对边分别为 ,且满足
,且满足


 的值;
的值; 的值.
的值. 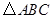 中,内角
中,内角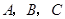 对边的边长分别是
对边的边长分别是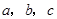 ,已知
,已知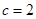 ,
,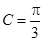 .
.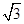 ,求
,求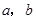 ;
;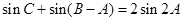 ,求
,求 ,
, ,
, 。
。 的值;
的值; 中,内角
中,内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且
,且
 的最大值.
的最大值.  的内角
的内角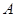 、
、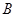 、
、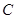 的对边分别为
的对边分别为 、
、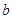 、
、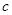 ,已知
,已知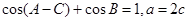 ,求
,求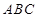 中,角
中,角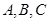 所对的边分别为
所对的边分别为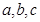 ,已知
,已知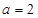 ,
, ,
,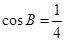 .
.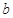 的值;
的值;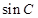 的值.
的值.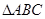 的面积
的面积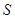 满足
满足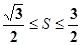 ,且
,且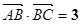 ,
,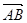 与
与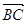 的夹角为
的夹角为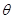 .
. 的最大值及最小值.
的最大值及最小值.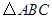 中,内角
中,内角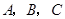 对边的边长分别是
对边的边长分别是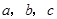 , 且
, 且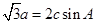
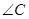
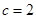 ,
, 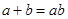 ,求ΔABC的面积
,求ΔABC的面积