题目内容
在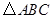 中,内角
中,内角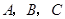 对边的边长分别是
对边的边长分别是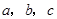 ,已知
,已知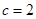 ,
,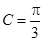 .
.
(Ⅰ)若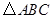 的面积等于
的面积等于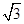 ,求
,求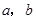 ;
;
(Ⅱ)若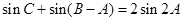 ,求
,求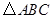 的面积.
的面积.
(Ⅰ)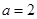 ,
,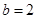 . (Ⅱ)
. (Ⅱ)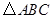 的面积
的面积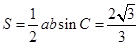 .
.
解析试题分析:(Ⅰ)由余弦定理及已知条件得,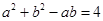 , 2分
, 2分
又因为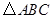 的面积等于
的面积等于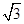 ,所以
,所以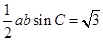 ,得
,得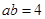 . 4分
. 4分
联立方程组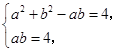 解得
解得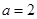 ,
,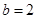 . 6分
. 6分
(Ⅱ)由题意得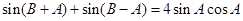 ,
,
即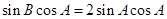 8分
8分
当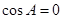 时,
时,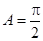 ,
,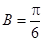 ,
,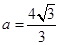 ,
,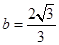 10分
10分
当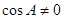 时,得
时,得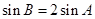 ,由正弦定理得
,由正弦定理得 ,
,
联立方程组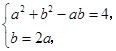 解得
解得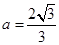 ,
,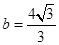 . 12分
. 12分
所以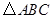 的面积
的面积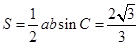 . 13分
. 13分
(注:缺一解统一扣3分)
考点:本题主要考查正弦定理、余弦定理的应用,三角形面积公式,两角和与差的三角函数。
点评:中档题,利用函数方程思想,运用正弦定理、余弦定理及三角形面积公式,建立a,b的方程组,使问题得到解决。计算要准确。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的边BC上一点,且
的边BC上一点,且
 ,且
,且 ,求BD的长。
,求BD的长。 =(sinA,b+c),
=(sinA,b+c), =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足 =
= (Ⅰ)求角B的大小;(Ⅱ)设
(Ⅰ)求角B的大小;(Ⅱ)设 =(sin(C+
=(sin(C+ ),
), ),
),  =(2k,cos2A) (k>1),
=(2k,cos2A) (k>1),  有最大值为3,求k的值.
有最大值为3,求k的值. 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且 .
. ;
; asin C=bsin B.
asin C=bsin B. 中,角
中,角 所对的边分别为
所对的边分别为 ,满足
,满足 .
. ;
;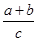 的取值范围.
的取值范围. 。
。