题目内容
已知函数
(1)若 在区间[1,+∞)上是增函数,求实数a的取值范围;
在区间[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=- 是
是 的极值点,求
的极值点,求 在[1,a]上的最大值;
在[1,a]上的最大值;
(3)在(2)的条件下,是否存在实数b,使得函数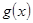 =bx的图象与函数
=bx的图象与函数 的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
【答案】
(1)a≤0
(2)-6
(3)b的范围为b>-7且b≠-3
【解析】解 (1)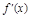 =3x2-2ax-3,∵f(x)在[1,+∞)上是增函数,
=3x2-2ax-3,∵f(x)在[1,+∞)上是增函数,
∴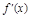 在[1,+∞)上恒有
在[1,+∞)上恒有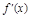 ≥0,
≥0,
即3x2-2ax-3≥0在[1,+∞)上恒成立.则必有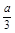 ≤1且
≤1且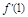 =-2a≥0,∴a≤0.
=-2a≥0,∴a≤0.
(2)依题意, =0,即
=0,即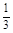 +
+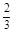 a-3=0,∴a=4,∴f(x)=x3-4x2-3x.令
a-3=0,∴a=4,∴f(x)=x3-4x2-3x.令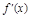 =3x2-8x-3=0,得x1=-
=3x2-8x-3=0,得x1=-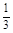 ,x2=3.
,x2=3.
则当x变化时, ,f(x)的变化情况如下表:
,f(x)的变化情况如下表:
|
x |
1 |
(1,3) |
3 |
(3,4) |
4 |
|
|
|
- |
0 |
+ |
|
|
f(x) |
-6 |
↘ |
-18 |
↗ |
-12 |
∴f(x)在[1,4]上的最大值是f(1)=-6.
(3)函数g(x)=bx的图象与函数f(x)的图象恰有3个交点,即方程x3-4x2-3x=bx恰有3个不等实根
∴x3-4x2-3x-bx=0,∴x=0是其中一个根,∴方程x2-4x-3-b=0有两个非零不等实根,
∴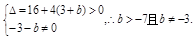 ∴存在符合条件的实数b,b的范围为b>-7且b≠-3.
∴存在符合条件的实数b,b的范围为b>-7且b≠-3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,
 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: .
.
 .
. 为
为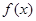 的极值点,求实数
的极值点,求实数 的值;
的值; 在
在 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值. 。
。 ,求函数
,求函数 的值;
的值; .
.
 中任取一个元素
中任取一个元素 ,从集合
,从集合 中任取一个元素
中任取一个元素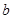 ,求方程
,求方程 有两个不相等实根的概率;
有两个不相等实根的概率; 中任取的一个数,
中任取的一个数, 中任取的一个数,求方程
中任取的一个数,求方程