Question

【题目】已知等比数列{an}的公比q=2，前3项和是7，等差数列{bn}满足b1=3，2b2=a2+a4 ． （Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）求数列 的前n项和Sn ．

Answer 1

【答案】解：（Ⅰ）∵等比数列{an}的公比q=2，前3项和是7，

∴a1+2a1+4a1=7，

∴a1=1，

∴an=2n﹣1，

设等差数列{bn}的公差为d，

∵b1=3，2b2=a2+a4=2+8，

∴b2=5，

∴d=5﹣3=2，

∴bn=3+2（n﹣1）=2n+1；

（Ⅱ） = = ﹣ ，

∴数列 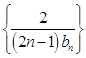的前n项和Sn=1﹣ + ﹣ +…+ ﹣ =1﹣ =

【解析】（Ⅰ）根据等差数列和等比数列的定义以及等比数列的求和公式即可求出通项公式，（Ⅱ） = = ﹣ ，裂项求和即可．
【考点精析】通过灵活运用数列的前n项和，掌握数列{an}的前n项和sn与通项an的关系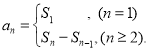即可以解答此题．