题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]()
![]() ,点P为直线l:
,点P为直线l:![]() 上且不在x轴上的任意一点,直线
上且不在x轴上的任意一点,直线![]() 和
和![]() 与椭圆的交点分别为A、B和C、D、O为坐标原点.
与椭圆的交点分别为A、B和C、D、O为坐标原点.
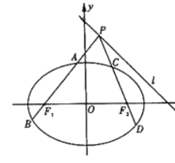
(1)求![]() 的周长;
的周长;
(2)设直线![]()
![]() 的斜线分别为
的斜线分别为![]()
![]() ,证明:
,证明:![]() ;
;
(3)问直线l上是否存在点P,使得直线OA、OB、OC、OD的斜率![]() 满足
满足![]() ?若存在,求出所有满足条件的点P的坐标;若不存在,说明理由.
?若存在,求出所有满足条件的点P的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)见解析;(3)存在,
;(2)见解析;(3)存在,![]() 或
或![]()
【解析】
(1)根据椭圆定义可知所求三角形周长为![]() ,结合椭圆方程可得到结果;
,结合椭圆方程可得到结果;
(2)由椭圆方程可知焦点坐标,设![]() ,利用两点连线斜率公式表示出
,利用两点连线斜率公式表示出![]() ,代入整理可得结论;
,代入整理可得结论;
(3)假设存在点![]() 满足题意,假设直线
满足题意,假设直线![]() :
:![]() ,与椭圆方程联立,利用韦达定理的表示出
,与椭圆方程联立,利用韦达定理的表示出![]() ,同理可得
,同理可得![]() ,由
,由![]() 可得到关于
可得到关于![]() 的方程;根据(2)中结论知
的方程;根据(2)中结论知![]() ,联立求得
,联立求得![]() ,进而得到两直线方程,两直线方程联立可求得满足题意的
,进而得到两直线方程,两直线方程联立可求得满足题意的![]() 点坐标.
点坐标.
(1)由椭圆定义知:![]()
![]() 的周长为:
的周长为:![]()
(2)由题意得:![]() ,
,![]() ,设
,设![]()
![]() ,
,![]()
![]()
(3)假设存在点![]() ,使得
,使得![]()
设![]() ,
,![]() ,
,![]() ,
,![]()
设直线![]() :
:![]() ;直线
;直线![]() :
:![]()
联立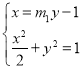 得:
得:![]()
![]() ,
,![]()
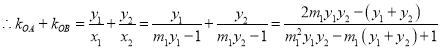
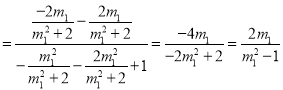
同理可得:![]()
![]() …①
…①
由(2)知,![]() …②
…②
①②联立可解得: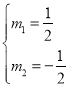 或
或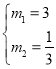
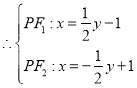 或
或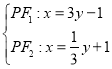
![]() 或
或![]()
![]() 存在点
存在点![]() 或
或![]() ,使得
,使得![]()

练习册系列答案
相关题目
【题目】已知某单位全体员工年龄频率分布表,经统计,该单位35岁以下的青年职工中,男职工和女职工人数相等,且男职工的年龄频率分布直方图和如下:
年龄(岁) | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) | [50,55) | 合计 |
人数(人) | 6 | 18 | 50 | 31 | 19 | 16 | 140 |
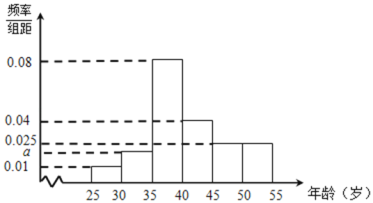
(Ⅰ)求![]() ;
;
(Ⅱ)求该单位男女职工的比例;
(Ⅲ)若从年龄在[25,30)岁的职工中随机抽取两人参加某项活动,求恰好抽取一名男职工和一名女职工的概率.