题目内容
【题目】某工厂有甲,乙两个车间生产同一种产品,,甲车间有工人![]() 人,乙车间有工人
人,乙车间有工人![]() 人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:
人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:![]() )进行统计,按照
)进行统计,按照![]() 进行分组,得到下列统计图.
进行分组,得到下列统计图.
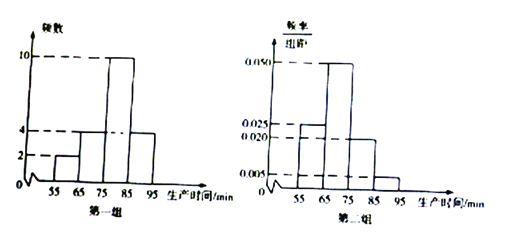
![]() 分别估算两个车间工人中,生产一件产品时间少于
分别估算两个车间工人中,生产一件产品时间少于![]() 的人数
的人数
![]() 分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
![]() 从第一组生产时间少于
从第一组生产时间少于![]() 的工人中随机抽取
的工人中随机抽取![]() 人,记抽取的生产时间少于
人,记抽取的生产时间少于![]() 的工人人数为随机变量
的工人人数为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】![]() 60,300;
60,300;![]() 乙车间工人生产效率更高;
乙车间工人生产效率更高;![]() 见解析.
见解析.
【解析】
(Ⅰ)由图表分别计算出两个车间生产一件产品时间少于![]() 的人数;
的人数;
(Ⅱ)分别计算两个车间工人生产一件产品时间的平均值,从而得到结果;
(Ⅲ)![]() 可取值为
可取值为![]() .计算出相应的概率值,得到分布列与期望.
.计算出相应的概率值,得到分布列与期望.
(Ⅰ)由题意得,第一组工人![]() 人,其中在
人,其中在![]() 内(不含
内(不含![]() )生产完成一件产品的有
)生产完成一件产品的有![]() 人
人
![]() 甲车间工人中生产一件产品时间少于
甲车间工人中生产一件产品时间少于![]() 的人数为
的人数为![]() (人)
(人)
第二组工人![]() 人. 其中在
人. 其中在![]() 内(不含
内(不含![]() )生产完成一件产品的有
)生产完成一件产品的有![]() 人
人
![]() 乙车间工人中生产一件产品时间少于
乙车间工人中生产一件产品时间少于![]() 的人数为
的人数为![]() (人)
(人)
(Ⅱ)第一组平均时间为![]() .
.
第二组平均时间为![]() .
.
![]() ,
,![]() 乙车间工人生产效率更高;
乙车间工人生产效率更高;
(Ⅲ)由题意得,第一组生产时间少于![]() 的工人有
的工人有![]() 人,从中抽取
人,从中抽取![]() 人,其中生产时间少于
人,其中生产时间少于![]() 的有
的有![]() 人.
人.
![]() 可取值为
可取值为![]() .
.
![]() .
.
![]() ,
,
![]() ,
,
![]() 的分布列为:
的分布列为:
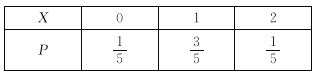
数学期望![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某高校在2019年的自主招生笔试成绩(满分200分)中,随机抽取100名考生的成绩,按此成绩分成五组,得到如下的频率分布表:
组号 | 分组 | 频数 | 频率 |
第一组 |
| 15 |
|
第二组 |
| 25 | 0.25 |
第三组 |
| 30 | 0.3 |
第四组 |
|
|
|
第五组 |
| 10 | 0.1 |
(1)求频率分布表中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估计笔试成绩的平均数及中位数(同一组中的数据用该组区间的中点值作代表);(精确到0.1)
(3)若从第四组、第五组的学生中按组用分层抽样的方法抽取6名学生参加面试,用简单随机抽样方法从6人中抽取2人作为正、副小组长,求“抽取的2人为同一组”的概率.
【题目】某校共有学生2000人,其中男生1100人,女生900人为了调查该校学生每周平均课外阅读时间,采用分层抽样的方法收集该校100名学生每周平均课外阅读时间(单位:小时)
(1)应抽查男生与女生各多少人?
(2)如图,根据收集100人的样本数据,得到学生每周平均课外阅读时间的频率分布直方图,其中样本数据分组区间为![]() .若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
.若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
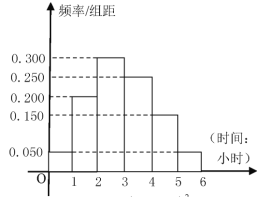
男生 | 女生 | 总计 | |
每周平均课外阅读时间不超过2小时 | |||
每周平均课外阅读时间超过2小时 | |||
总计 |
附:
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
【题目】某企业为了检查生产![]() 产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.下表是甲流水线样本的频数分布表,下图是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.下表是甲流水线样本的频数分布表,下图是乙流水线样本的频率分布直方图.
甲流水线样本的频数分布表
质量指标值 | 频数 |
| 9 |
| 10 |
| 17 |
| 8 |
| 6 |
乙流水线样本的频率分布直方图
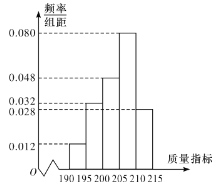
(1)根据图形,估计乙流水线生产的![]() 产品的该项质量指标值的中位数;
产品的该项质量指标值的中位数;
(2)设该企业生产一件合格品获利100元,生产一件不合格品亏损50元,若某个月内甲、乙两条流水线均生产了1000件产品,若将频率视为概率,则该企业本月的利润约为多少元?