题目内容
13.已知向量$\overrightarrow{a}$=(2x+1,3),$\overrightarrow{b}$=(2,2-x),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数x的值等于-8.分析 利用垂直向量的数量积为0的性质求解.
解答 解:∵向量$\overrightarrow{a}$=(2x+1,3),$\overrightarrow{b}$=(2,2-x),a⊥b,
∴$\overrightarrow{a}•\overrightarrow{b}$=2(2x+1)+3(2-x)=0,
解得x=-8.
故答案为:-8.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意向量垂直的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.若函数$f(x)=\left\{\begin{array}{l}sinx+\frac{3}{2},x≥0\\{x^2}+a,x<0\end{array}\right.$(其中a∈R)的值域为$[\frac{1}{2},+∞)$,则a的取值范围是( )
| A. | $[\frac{3}{2},+∞)$ | B. | $[\frac{1}{2},\frac{3}{2}]$ | C. | $[\frac{1}{2},\frac{5}{2}]$ | D. | $[\frac{1}{2},+∞)$ |
1.“lgx>lgy”是“$\sqrt{x}$>$\sqrt{y}$”的( )
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
2.已知i为虚数单位,则|$\frac{2+4i}{1+\sqrt{3}i}$|=( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 5 |
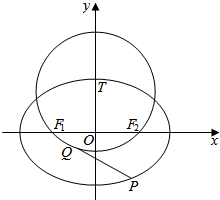 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点M(1,$\frac{\sqrt{2}}{2}$),离心率e=$\frac{\sqrt{2}}{2}$,F1、F2为椭圆的左、右焦点.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点M(1,$\frac{\sqrt{2}}{2}$),离心率e=$\frac{\sqrt{2}}{2}$,F1、F2为椭圆的左、右焦点.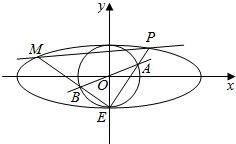 如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0)和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π,椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A、B,直线EA、EB与椭圆C1的另一个交点分别是点P、M.
如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0)和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π,椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A、B,直线EA、EB与椭圆C1的另一个交点分别是点P、M.