题目内容
已知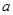 为常数,若曲线
为常数,若曲线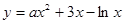 存在与直线
存在与直线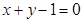 垂直的切线,则实数
垂直的切线,则实数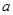 的取值范围是( )
的取值范围是( )
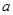 为常数,若曲线
为常数,若曲线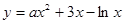 存在与直线
存在与直线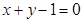 垂直的切线,则实数
垂直的切线,则实数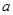 的取值范围是( )
的取值范围是( )A.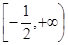 | B.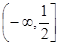 | C.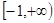 | D.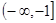 |
A
试题分析:因为直线x+y-1=0直线的斜率为-1,那么所求的曲线的切线的斜率为1,故设切点为(m,n),则因为f’(x)=2ax+3-
 =1方程有解,同时要助于定义域x>0,那么分离参数2ax=
=1方程有解,同时要助于定义域x>0,那么分离参数2ax= -2,可得a=
-2,可得a=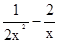 (x>0),求解右边函数的值域即为参数a的范围。则根据
(x>0),求解右边函数的值域即为参数a的范围。则根据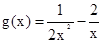 ,结合二次函数的性质可知其范围是a
,结合二次函数的性质可知其范围是a ,故选A.
,故选A.点评:解决该试题的关键是利用两条直线的垂直关系,得到切线的斜率值,然后利用导数的几何意义,得到该点的导数值。进而方程有解得到a的范围。

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
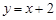 上的一点向圆
上的一点向圆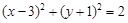 引切线,则切线长的最小值为
引切线,则切线长的最小值为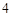
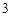
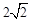
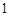
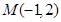 在直线
在直线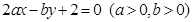 上,则
上,则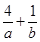 的最小值是( )
的最小值是( )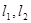 的倾斜角分别为
的倾斜角分别为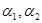 ,则下列四个命题中正确的是( )
,则下列四个命题中正确的是( ) ,则两直线的斜率:
,则两直线的斜率: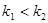
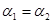 ,则两直线的斜率:
,则两直线的斜率: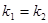
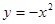 上的点到直线
上的点到直线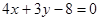 的距离的最小值是
的距离的最小值是 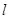 的一个法向量为
的一个法向量为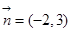 ,且经过点
,且经过点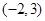 ,则直线
,则直线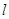 过点
过点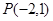 且斜率为
且斜率为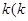 >
>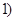 ,将直线
,将直线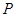 点按逆时针方向旋转45°得直线
点按逆时针方向旋转45°得直线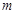 ,若直线
,若直线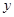 轴交于
轴交于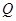 ,
,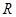 两点.(1)用
两点.(1)用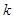 表示直线
表示直线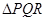 的面积最小?并求出面积最小时直线
的面积最小?并求出面积最小时直线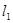 :
: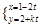 (
( 为参数)与直线
为参数)与直线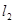 :
: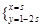 (
(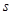 为参数)垂直,则
为参数)垂直,则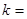 _________________.
_________________.