题目内容
设等差数列{an}的前n项和为Sn,若a1=-5,且它的前11项的平均值是5.
(1)求等差数列的公差d;
(2)求使Sn>0成立的最小正整数n.
(本小题满分14分)
解:(1)∵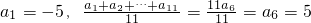
∴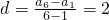 .…(7分)
.…(7分)
(2)∵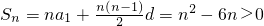
∴n>6且n∈N*,∴使Sn>0成立的最小正整数n为7.…(14分)
分析:(1)由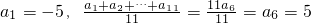 可求d
可求d
(2)由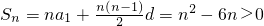 可得n的范围,结合n为正整数可求
可得n的范围,结合n为正整数可求
点评:本题主要考查了等差数量的通项公式、等差数列的性质及求和公式的应用,属于基础性试题.
解:(1)∵
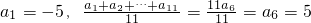
∴
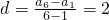 .…(7分)
.…(7分)(2)∵
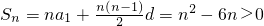
∴n>6且n∈N*,∴使Sn>0成立的最小正整数n为7.…(14分)
分析:(1)由
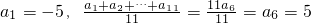 可求d
可求d(2)由
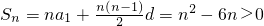 可得n的范围,结合n为正整数可求
可得n的范围,结合n为正整数可求点评:本题主要考查了等差数量的通项公式、等差数列的性质及求和公式的应用,属于基础性试题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目