题目内容
(本小题共13分)
已知函数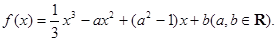
(I)若x=1为 的极值点,求a的值;
的极值点,求a的值;
(II)若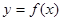 的图象在点(1,
的图象在点(1, )处的切线方程为
)处的切线方程为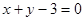 ,
,
(i)求 在区间[-2,4]上的最大值;
在区间[-2,4]上的最大值;
(ii)求函数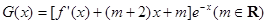 的单调区间.
的单调区间.
(I)0或2
(II)(i)8
(ii)当m=2时,G(x)在(-∞,+∞)单调递减;
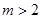 时,G(x)在(-∞,2-m),(0,+∞)单调递减,在(2-m,0)单调递增;
时,G(x)在(-∞,2-m),(0,+∞)单调递减,在(2-m,0)单调递增;
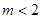 时,G(x)在(-∞,0),(2-m,+∞)单调递减,在(0,2-m)单调递增.
时,G(x)在(-∞,0),(2-m,+∞)单调递减,在(0,2-m)单调递增.
【解析】(I)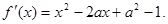
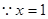 是极值点
是极值点
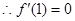 ,即
,即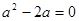
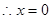 或2.…………………………………………………………3分
或2.…………………………………………………………3分
(II)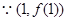 在
在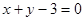 上.
上. 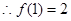
∵(1,2)在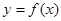 上
上 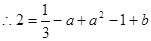
又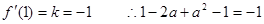
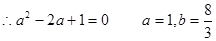
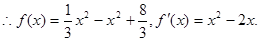
(i)由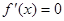 可知x=0和x=2是
可知x=0和x=2是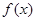 的极值点.
的极值点.
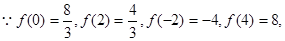
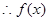 在区间[-2,4]上的最大值为8.…………………………8分
在区间[-2,4]上的最大值为8.…………………………8分
(ii)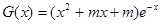
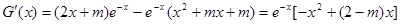
令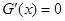 ,得
,得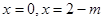
当m=2时,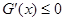 ,此时
,此时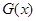 在
在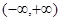 单调递减
单调递减
当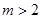 时:
时:
|
x |
(-∞,2,-m) |
2-m |
(2-m,0) |
0 |
(0,+∞) |
|
G′(x) |
- |
0 |
+ |
0 |
- |
|
G(x) |
减 |
|
增 |
|
减 |
当时G(x)在(-∞,2,-m),(0,+∞)单调递减,在(2-m,0)单调递增.
当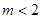 时:
时:
|
x |
(-∞,0) |
0 |
(0,2-m) |
2-m |
(2-m+∞) |
|
G′(x) |
- |
0 |
+ |
0 |
- |
|
G(x) |
减 |
|
增 |
|
减 |
此时G(x)在(-∞,0),(2-m+∞)单调递减,在(0,2-m)单调递增,综上所述:当m=2时,G(x)在(-∞,+∞)单调递减;
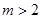 时,G(x)在(-∞,2-m),(0,+∞)单调递减,在(2-m,0)单调递增;
时,G(x)在(-∞,2-m),(0,+∞)单调递减,在(2-m,0)单调递增;
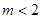 时,G(x)在(-∞,0),(2-m,+∞)单调递减,在(0,2-m)单调递增.
时,G(x)在(-∞,0),(2-m,+∞)单调递减,在(0,2-m)单调递增.
………………………………………………………………13分

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 .
. 在
在 处取得极值,求a的值;
处取得极值,求a的值; 在
在 上的最大值.
上的最大值. ,设函数
,设函数 .
. 在
在 上的单调递增区间;
上的单调递增区间; 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,
的对边, ,
, ,
, ,求边
,求边 ,求
,求
 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式; 的条件下,求
的条件下,求 的值.
的值.