Question

点P（x，y）满足(x-1)2+y2≤1且

x-y≥0 x+y≥0

，则y-2x的最大值与最小值分别为（　　）

• A、

  5

  -2，-

  5

  -2
• B、1，-

  5

  -2
• C、

  5

  -2，1
• D、0，-

  5

  -2

Answer 1

分析：根据已知中的约束条件，画出满足(x-1)2+y2≤1且

x-y≥0 x+y≥0

，的平面区域，并画出满足条件的可行域，由图我们易求出平面区域的各角点的坐标，将角点坐标代入目标函数易判断出目标函数y-2x的最大值和最小值．

解答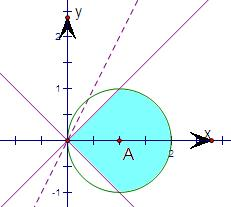：解：满足(x-1)2+y2≤1且

x-y≥0 x+y≥0

，的平面区域如下图所示：
由图可知：
当直线与圆在下方相切时y-2x取最小，最小值为：=-

5

-2
当x=0，y=0时y-2x取最大值0．
故选D．

点评：本题考查的知识点是简单线性规划，画出满足条件的可行域及利用直线与圆的位置关系是解答线性规划类小题的关键．