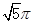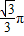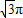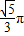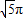题目内容
已知圆锥底面半径为1,它的侧面展开图是一个圆心角为90°的扇形,则圆锥的表面积是( )
分析:根据圆锥的底面圆周长等于侧面展开扇形的弧长,利用扇形的弧长公式算出母线长l=4,再利用圆锥的侧面积公式和底面积公式加以计算,即可得到该圆锥的表面积.
解答:解:∵圆锥底面半径为r=1,∴圆锥的底面周长为2πr=2π,
设圆锥的母线长为l,则
∵圆锥的侧面展开图是一个圆心角为90°的扇形,
∴
=2π,解之得l=4.
因此可得圆锥的表面积S=S侧+S底=πrl+πr2=4π+π=5π,
故选:B
设圆锥的母线长为l,则
∵圆锥的侧面展开图是一个圆心角为90°的扇形,
∴
| 90πl |
| 180 |
因此可得圆锥的表面积S=S侧+S底=πrl+πr2=4π+π=5π,
故选:B
点评:本题给出圆锥的底面圆半径和展开扇形的圆心角,求圆锥的表面积.着重考查了弧长公式、圆锥的侧面积公式等知识属于中档题.

练习册系列答案
相关题目
 已知如图所示圆锥的母线长为6,底面半径为1,现有一只蚂蚁从底面圆的A点出发,绕圆锥侧面一圈后回到点A,则这只蚂蚁爬过的最短距离为
已知如图所示圆锥的母线长为6,底面半径为1,现有一只蚂蚁从底面圆的A点出发,绕圆锥侧面一圈后回到点A,则这只蚂蚁爬过的最短距离为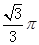 B.
B.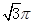 C.
C.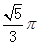
 D.
D.