题目内容
【题目】如图,A 为椭圆![]() 的下顶点,过 A 的直线 l 交抛物线
的下顶点,过 A 的直线 l 交抛物线![]() 于B、C 两点,C 是 AB 的中点.
于B、C 两点,C 是 AB 的中点.
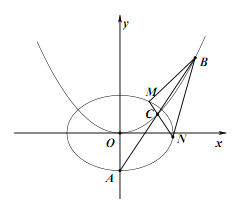
(I)求证:点C的纵坐标是定值;
(II)过点C作与直线 l 倾斜角互补的直线l交椭圆于M、N两点,求p的值,使得△BMN的面积最大.
【答案】(Ⅰ)见证明;(II)见解析
【解析】
(I)根据点在抛物线上设出B的坐标,可表示出C的坐标,代入抛物线方程求得纵坐标.
(II)先利用条件得到![]() ,联立直线
,联立直线![]() 与椭圆的方程,求得弦长
与椭圆的方程,求得弦长![]() 及
及![]() 到
到![]() 的距离,写出面积的表达式,利用基本不等式求得最值及相应的参数即可.
的距离,写出面积的表达式,利用基本不等式求得最值及相应的参数即可.
(Ⅰ)易知![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
,
代入抛物线方程得:
![]() ,得:
,得:![]() ,
,![]() 为定值.
为定值.
(Ⅱ)![]() 点
点![]() 是
是![]() 中点,
中点,![]()
![]() 直线
直线![]() 的斜率
的斜率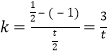 ,直线
,直线![]() 的斜率
的斜率![]() ,
,
![]() 直线
直线![]() 的方程:
的方程:![]() ,即
,即![]() ,
,
不妨记![]() ,则
,则![]() :
:![]()
代入椭圆方程整理得:![]() ,
,
设![]() ,则
,则
![]() ,
,![]() ,
,
![]() ,
,
![]() 到
到![]() 的距离
的距离![]() ,
,
所以![]()
![]()
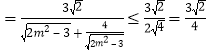 .
.
取等号时,![]() ,得
,得![]() ,所以
,所以![]() ,
,![]() .
.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目