题目内容

1．已知等差数列{an}的前n项和为Sn，且满足S3=6，S6=3．则S9=-9．

分析 由等差数列的性质可得S3，S6-S3，S9-S6成等差数列，可得2（S6-S3）=S3+S9-S6，代值计算可得．

解答 解：由等差数列的性质可得S3，S6-S3，S9-S6成等差数列，
∴2（S6-S3）=S3+S9-S6，即2（3-6）=6+S9-3，
解得S9=-9，
故答案为：-9．

点评 本题考查等差数列的求和公式和性质，属基础题．

练习册系列答案
相关题目
11．已知$|{\overrightarrow a}|=1，|{\overrightarrow b}|=6，\overrightarrow a•（{\overrightarrow b-\overrightarrow a}）=2$，则$\overrightarrow a$和$\overrightarrow b$的夹角为（　　）
A．30°B．45°C．60°D．90°
12．已知直线l丄平面α，直线m?平面β给出下列命题：
①α∥β=＞l丄m；②α丄β=＞l∥m；
③l∥m=＞α丄β；④l丄m=＞α∥β；
其中正确命题的序号是（　　）
A．①②③B．②③④C．①③D．②④
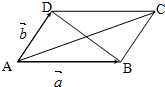9．如图在平行四边形ABCD中，M，N分别为DC，BC的中点，已知$\overrightarrow{AB}$=$\overrightarrow a$，$\overrightarrow{AD}$=$\overrightarrow b$，试用$\overrightarrow a$，$\overrightarrow{b}$表示$\overrightarrow{AC}，\overrightarrow{BD}，\overrightarrow{AM，}\overrightarrow{AN}$，$\overrightarrow{NM}，\overrightarrow{MB}$．
16．在△ABC中，角A，B，C所对的边分别为a，b，c，其中C角为钝角．cos（A+B-C）=$\frac{1}{4}$，a=2，$\frac{{sin（{B+A}）}}{sinA}$=2．
（1）求cosC的值；
（2）求b的长．
6．计算i•i2•i3•i4•…•i2015=1．
13．已知$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-2，m），若$\overrightarrow{a}⊥\overrightarrow{b}$，则实数m的值为（　　）
A．1B．4C．-4D．-1
10．关于实数x的不等式-x2+bx+c＜0的解集是{x|x＜-3或x＞2}，则关于x的不等式cx2-bx-1＞0的解集是（　　）
A．（-$\frac{1}{2}$，$\frac{1}{3}$）B．（-2，3）C．（-∞，-$\frac{1}{2}$）∪（$\frac{1}{3}$，+∞）D．（-∞，-2）∪（3，+∞）
11．若a${\;}^{\frac{3}{4}}$$＞{a}^{\frac{5}{4}}$，则实数a的取值范围是（0，1）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网