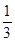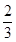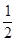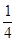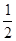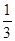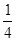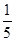题目内容
一投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分.经过多次试验,某人投掷100个飞碟有50个入红袋,25个入蓝袋,其余不能入袋.
(1)求该人在4次投掷中恰有三次投入红袋的概率;
(2)求该人两次投掷后得分ξ的数学期望Eξ.
(1)求该人在4次投掷中恰有三次投入红袋的概率;
(2)求该人两次投掷后得分ξ的数学期望Eξ.
(1)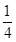 (2)
(2)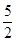
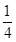 (2)
(2)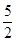
(1)“飞碟投入红袋”,“飞碟投入蓝袋”,“飞碟不入袋”分别记为事件A,B,C.
则P(A)=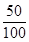 =
=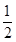 ,P(B)=P(C)=
,P(B)=P(C)=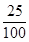 =
=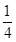 .
.
因每次投掷飞碟为相互独立事件,故4次投掷中恰有三次投入红袋的概率为P4(3)=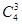
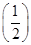 3
3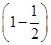 =
=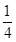 .
.
(2)两次投掷得分ξ的得分可取值为0,1,2,3,4则:
P(ξ=0)=P(C)P(C)=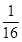 ;
;
P(ξ=1)=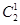 P(B)P(C)=2×
P(B)P(C)=2×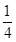 ×
×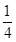 =
=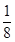 ;
;
P(ξ=2)=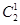 P(A)P(C)+P(B)P(B)=
P(A)P(C)+P(B)P(B)=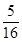 ;
;
P(ξ=3)=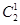 P(A)P(B)=
P(A)P(B)=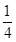 ;
;
P(ξ=4)=P(A)P(A)=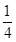 .
.
∴E(ξ)=0×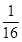 +1×
+1×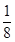 +2×
+2×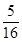 +3×
+3×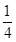 +4×
+4×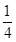 =
=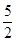 .
.
则P(A)=
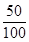 =
=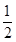 ,P(B)=P(C)=
,P(B)=P(C)=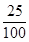 =
=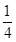 .
.因每次投掷飞碟为相互独立事件,故4次投掷中恰有三次投入红袋的概率为P4(3)=
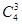
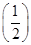 3
3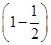 =
=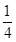 .
.(2)两次投掷得分ξ的得分可取值为0,1,2,3,4则:
P(ξ=0)=P(C)P(C)=
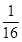 ;
;P(ξ=1)=
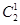 P(B)P(C)=2×
P(B)P(C)=2×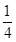 ×
×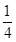 =
=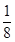 ;
;P(ξ=2)=
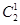 P(A)P(C)+P(B)P(B)=
P(A)P(C)+P(B)P(B)=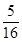 ;
;P(ξ=3)=
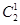 P(A)P(B)=
P(A)P(B)=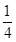 ;
;P(ξ=4)=P(A)P(A)=
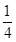 .
.∴E(ξ)=0×
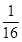 +1×
+1×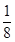 +2×
+2×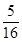 +3×
+3×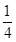 +4×
+4×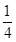 =
=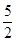 .
.
练习册系列答案
相关题目
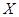 ,求
,求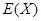 .
.