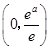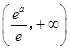Question

【题目】已知函数f（x）=lnx﹣a（a∈R）与函数 有公共切线． （Ⅰ）求a的取值范围；
（Ⅱ）若不等式xf（x）+e＞2﹣a对于x＞0的一切值恒成立，求a的取值范围．

Answer 1

【答案】解：（Ⅰ） ， ． ∵函数f（x）与F（x）有公共切线，∴函数f（x）与F（x）的图象相切或无交点．
当两函数图象相切时，设切点的横坐标为x0（x0＞0），则 ，
解得x0=2或x0=﹣1（舍去），
则f（2）=F（2），得a=ln2﹣3，
由此求出a≥ln2﹣3，即a的取值范围为[ln2﹣3，+∞）．
（Ⅱ）等价于xlnx+a+e﹣2﹣ax≥0在x∈（0，+∞）上恒成立，
令g（x）=xlnx+a+e﹣2﹣ax，
因为g'（x）=lnx+1﹣a，令g'（x）=0，得 ，

x
g'（x）	﹣	0	+
g（x）		极小值

所以g（x）的最小值为 ，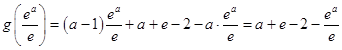
令 ，因为 ，
令t'（x）=0，得x=1，且

x	（0，1）	1	（1，+∞）
t'（x）	+	0	﹣
t（x）		极大值

所以当a∈（0，1）时，g（x）的最小值 ，
当a∈[1，+∞）时，g（x）的最小值为 =t（2），
所以a∈[1，2]．
综上得a的取值范围为（0，2]
【解析】．（Ⅰ） ， ．由函数f（x）与F（x）有公共切线，知函数f（x）与F（x）的图象相切或无交点．由此能求出a的取值范围（Ⅱ）等价于xlnx+a+e﹣2﹣ax≥0在x∈（0，+∞）上恒成立，令g（x）=xlnx+a+e﹣2﹣ax，g'（x）=lnx+1﹣a，令g'（x）=0，得 ，从而求出g（x）的最小值，令 ，由 =0，得x=1，由此能求出a的取值范围．
【考点精析】根据题目的已知条件，利用利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识可以得到问题的答案，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减；求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值．