题目内容
已知集合A={y|y=x+8,x∈R},B={y|y=x2-x,x∈R},则A∩B为
- A.{-2,4}
- B.{(-2,6),(4,12)}
- C.
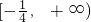
- D.R
C
分析:分别求出两集合中两函数的值域即可得到两集合,求出两集合的交集即可.
解答:因为y=x2-x=(x- )2-
)2- ≥-
≥- ,所以集合B=[-
,所以集合B=[- ,+∞),
,+∞),
又y=x+8∈R,所以集合A=R,
则A∩B=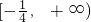 .
.
故选C.
点评:此题属于以函数的值域为平台,考查了求交集的运算,是一道基础题.
分析:分别求出两集合中两函数的值域即可得到两集合,求出两集合的交集即可.
解答:因为y=x2-x=(x-
 )2-
)2- ≥-
≥- ,所以集合B=[-
,所以集合B=[- ,+∞),
,+∞),又y=x+8∈R,所以集合A=R,
则A∩B=
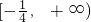 .
.故选C.
点评:此题属于以函数的值域为平台,考查了求交集的运算,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={y|y=log2x,x>1},B={y|y=(
)x,x>1},则A∪B等于( )
| 1 |
| 2 |
A、{y|0<y<
| ||
| B、{y|y>0} | ||
| C、∅ | ||
| D、R |