题目内容
给定数列
(1)判断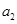 是否为有理数,证明你的结论;
是否为有理数,证明你的结论;
(2)是否存在常数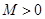 .使
.使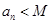 对
对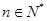 都成立? 若存在,找出
都成立? 若存在,找出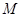 的一个值, 并加以证明; 若不存在,说明理由.
的一个值, 并加以证明; 若不存在,说明理由.
(1) 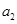 是无理数 (2)
是无理数 (2) 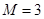 (或
(或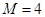 等).则对
等).则对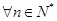 ,均有
,均有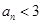 成立.证明略.
成立.证明略.
解析试题分析:(1) 设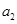 是无理数, 利用反证法推出矛盾即可;(2)先设
是无理数, 利用反证法推出矛盾即可;(2)先设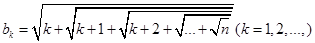 然后得到
然后得到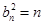 ,用放缩法证出
,用放缩法证出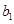
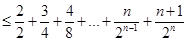 ,再借助错位相减法得
,再借助错位相减法得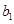 <3,即对
<3,即对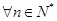 ,均有
,均有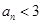 成立.
成立.
解:(1)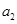 是无理数, 若不然,设
是无理数, 若不然,设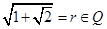 .
.
则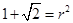 即
即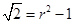 必为有理数,这与
必为有理数,这与 是无理数矛盾.
是无理数矛盾.
(2)设
则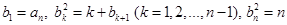 .
.
于是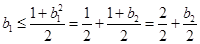
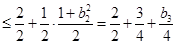
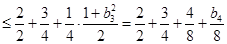
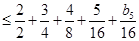
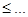
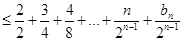
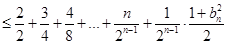
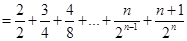
令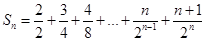 .
.
则 .
.
从而可取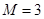 (或
(或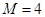 等).则对
等).则对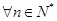 ,
,
均有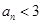 成立.
成立.
考点:反证法;错位相减法;放缩法.

练习册系列答案
相关题目
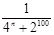 (n="1," 2, ),则S99=a1+a2+ +a99=
(n="1," 2, ),则S99=a1+a2+ +a99= 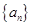 满足对任意的
满足对任意的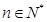 ,都有
,都有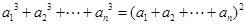 且
且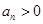 .
.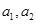 的值;
的值;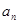 ;
;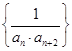 的前
的前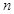 项和为
项和为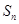 ,不等式
,不等式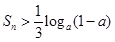 对任意的正整数
对任意的正整数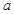 的取值范围.
的取值范围. 的首项
的首项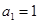 ,前
,前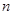 项和为
项和为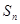 ,且
,且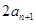 ,
,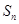 ,
,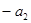 成等差数列,其中
成等差数列,其中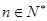 .
.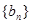 满足:
满足: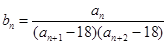 ,记数列
,记数列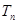 ,求
,求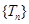 的最大项.
的最大项.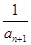 +
+ +
+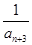 +…+
+…+ ,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+
,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+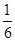 >bn恒成立,求实数t的取值范围.
>bn恒成立,求实数t的取值范围.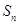 ,
,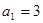 ,满足
,满足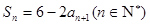 ,
,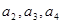 的值;
的值;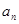 的表达式.
的表达式.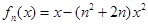 (其中
(其中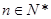 ),区间
),区间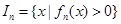 .
. 的长度(注:区间
的长度(注:区间 的长度定义为
的长度定义为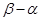 );
);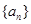 ,令
,令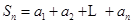 ,证明:
,证明: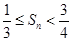 .
.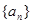 的首项
的首项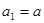 ,
,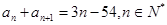
 项和为
项和为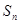 ,若
,若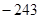 ,求
,求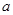 的取值范围?
的取值范围?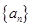 的前
的前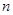 项和为
项和为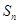 ,
,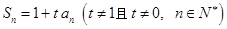 .
. ,求实数
,求实数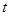 的取值范围.
的取值范围.