题目内容
已知函数![]() .
.
(1)若方程![]() 在区间
在区间![]() 内有两个不相等的实根,求实数
内有两个不相等的实根,求实数![]() 的取值范围;
的取值范围;
(2)如果函数![]() 的图像与x轴交于两点
的图像与x轴交于两点![]() ,且
,且![]() ,求证:
,求证:![]() (其中,
(其中,![]() 是
是![]() 的导函数,正常数
的导函数,正常数![]() 满足
满足![]() ).
).
解:(1)∵![]() ,
,![]() , -----1分
, -----1分
∴当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减。 ----3分
单调递减。 ----3分
∴当x=1时,![]() 有极大值,也是最大值,即为-1,但无最小值。
有极大值,也是最大值,即为-1,但无最小值。
故![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;最大值为-1,但无最小值。
;最大值为-1,但无最小值。
方程化为![]() , -----3分
, -----3分
由上知,![]() 在区间
在区间![]() 上的最大值为-1,
上的最大值为-1,![]() ,
,![]() ,
,![]() 。故
。故![]() 在区间
在区间![]() 上有两个不等实根需满足
上有两个不等实根需满足![]() ,
,
∴![]() ,∴实数m的取值范围为
,∴实数m的取值范围为![]() 。 -----6分
。 -----6分
(2)∵![]() ,又
,又![]() 有两个实根
有两个实根![]() ,
,
∴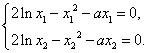 两式相减,得
两式相减,得![]()
∴![]() -----8分
-----8分
于是![]()
=![]() .
.
∵![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() 。 -----9分
。 -----9分
要证:![]() ,只需证:
,只需证:![]() .
.
只需证:![]() . (*)
. (*)
令![]() ,∴(*)化为
,∴(*)化为![]()
只证![]() 即可. -----11分
即可. -----11分
![]()
![]()
![]()
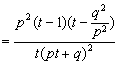 ,
,![]() ,0<t<1,
,0<t<1,
∴t-1<0.
∴u'(t)>0,∴u(t)在(0,1)上单调递增,∴u(t)<u(1)=0
∴u(t)<0,![]()
即:![]() .
.
![]() .............13分
.............13分

 ,
,
 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: .
.
 .
. 为
为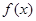 的极值点,求实数
的极值点,求实数 的值;
的值; 在
在 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值. 。
。 ,求函数
,求函数 的值;
的值; .
.
 中任取一个元素
中任取一个元素 ,从集合
,从集合 中任取一个元素
中任取一个元素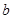 ,求方程
,求方程 有两个不相等实根的概率;
有两个不相等实根的概率; 中任取的一个数,
中任取的一个数, 中任取的一个数,求方程
中任取的一个数,求方程