题目内容
已知函数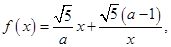
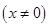
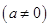
⑴试就实数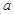 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;
⑵已知当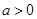 时,函数在
时,函数在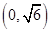 上单调递减,在
上单调递减,在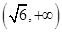 上单调递增,求
上单调递增,求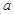 的值并写出函数的解析式;
的值并写出函数的解析式;
⑶若函数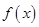 在区间
在区间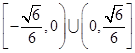 内有反函数,试求出实数
内有反函数,试求出实数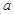 的取值范围。
的取值范围。
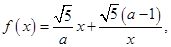
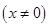
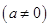
⑴试就实数
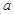 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;⑵已知当
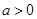 时,函数在
时,函数在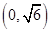 上单调递减,在
上单调递减,在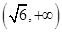 上单调递增,求
上单调递增,求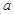 的值并写出函数的解析式;
的值并写出函数的解析式; ⑶若函数
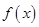 在区间
在区间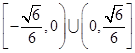 内有反函数,试求出实数
内有反函数,试求出实数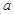 的取值范围。
的取值范围。(1) ①当
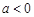 时,函数
时,函数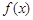 的单调递增区间为
的单调递增区间为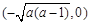 及
及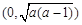 ,
, ②当
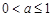 时,函数
时,函数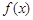 的单调递增区间为
的单调递增区间为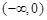 及
及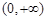 ,
,③当
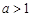 时,函数
时,函数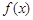 的单调递增区间为
的单调递增区间为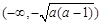 及
及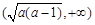 .
.(6)
(2) 由题设及(1)中③知
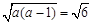 且
且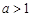 ,解得
,解得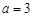 , (2)
, (2)因此函数解析式为
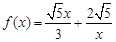
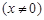 . (1)
. (1)(3)1# 当
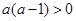 即
即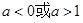 时
时由图象知
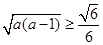 解得
解得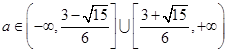
2# 当
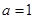 时,函数为正比例函数,故在区间内存在反函数,所以
时,函数为正比例函数,故在区间内存在反函数,所以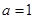 成立。
成立。3# 当
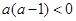 ,得到
,得到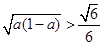 ,从而得
,从而得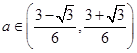
综上
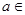
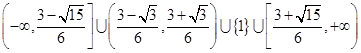 (9)
(9)略

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
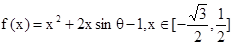
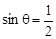 时,求f(x)的最大值与最小值;
时,求f(x)的最大值与最小值;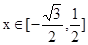 上是单调函数,且
上是单调函数,且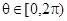 ,求θ的取值范围。
,求θ的取值范围。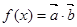 ,其中向量
,其中向量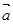 =(2cosx,1),
=(2cosx,1),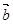 =(cosx,
=(cosx,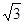 sin2x),x∈R.
sin2x),x∈R.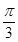 ,
,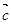 =(m,n)(|m|<
=(m,n)(|m|<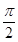 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.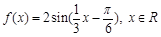 .
.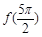 的值;
的值;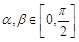 ,
,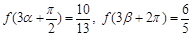 ,求
,求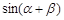 的值.
的值.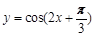 的图像,只需将函数
的图像,只需将函数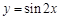 的图像
的图像
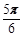 个长度单位
个长度单位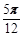 个长度单位
个长度单位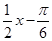 )的图象相邻的两条对称轴间的距离是
)的图象相邻的两条对称轴间的距离是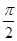
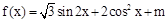 在区间[
在区间[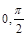 ]上的最大值为6,
]上的最大值为6,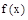 关于y轴的对称图象得函数
关于y轴的对称图象得函数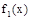 的图象,再把
的图象,再把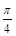 个单位得
个单位得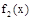 的图象,求函数
的图象,求函数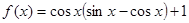 ,求
,求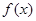 的值域和最小正周期。
的值域和最小正周期。