题目内容
(本题满分12分)设函数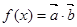 ,其中向量
,其中向量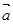 =(2cosx,1),
=(2cosx,1),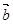 =(cosx,
=(cosx,
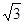 sin2x),x∈R.
sin2x),x∈R.
(1)若f(x)=1-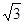 且x∈[-
且x∈[-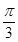 ,
,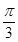 ],求x;
],求x;
(2)若函数y=2sin2x的图象按向量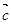 =(m,n)(|m|<
=(m,n)(|m|<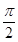 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
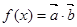 ,其中向量
,其中向量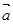 =(2cosx,1),
=(2cosx,1),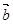 =(cosx,
=(cosx,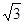 sin2x),x∈R.
sin2x),x∈R.(1)若f(x)=1-
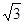 且x∈[-
且x∈[-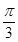 ,
,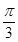 ],求x;
],求x;(2)若函数y=2sin2x的图象按向量
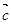 =(m,n)(|m|<
=(m,n)(|m|<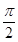 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.解:(1)依题设,f(x)=2cos2x+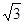 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+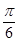 ). ……………2分
). ……………2分
由1+2sin(2x+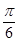 )=1-
)=1-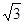 ,得sin(2x+
,得sin(2x+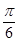 )=-
)=-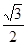 .……………4分
.……………4分
∵-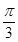 ≤x≤
≤x≤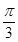 ,∴-
,∴-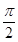 ≤2x+
≤2x+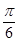 ≤
≤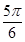 ,∴2x+
,∴2x+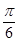 =-
=-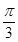 ,
,
即x=-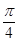 . .……………6分
. .……………6分
(2)函数y=2sin2x的图象按向量c=(m,n)平移后得到函数y=2sin2(x-m)+n的图象,
即函数y=f(x)的图象. .……………8分
由(1)得 f(x)=2sin2(x+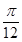 )+1. ∵|m|<
)+1. ∵|m|<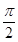 ,∴m=-
,∴m=-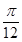 ,n="1. " .……………12分
,n="1. " .……………12分
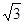 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+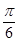 ). ……………2分
). ……………2分由1+2sin(2x+
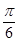 )=1-
)=1-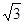 ,得sin(2x+
,得sin(2x+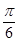 )=-
)=-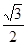 .……………4分
.……………4分∵-
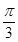 ≤x≤
≤x≤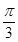 ,∴-
,∴-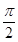 ≤2x+
≤2x+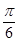 ≤
≤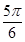 ,∴2x+
,∴2x+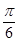 =-
=-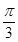 ,
, 即x=-
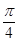 . .……………6分
. .……………6分(2)函数y=2sin2x的图象按向量c=(m,n)平移后得到函数y=2sin2(x-m)+n的图象,
即函数y=f(x)的图象. .……………8分
由(1)得 f(x)=2sin2(x+
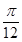 )+1. ∵|m|<
)+1. ∵|m|<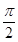 ,∴m=-
,∴m=-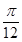 ,n="1. " .……………12分
,n="1. " .……………12分略

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
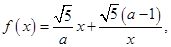
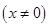
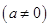
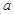 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;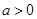 时,函数在
时,函数在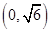 上单调递减,在
上单调递减,在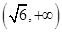 上单调递增,求
上单调递增,求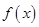 在区间
在区间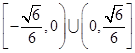 内有反函数,试求出实数
内有反函数,试求出实数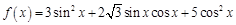 .
.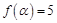 ,求
,求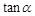 的值;
的值;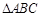 三内角
三内角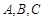 所对边分别为
所对边分别为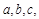 且
且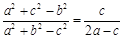 ,求
,求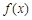 在
在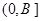 上的值域.
上的值域.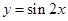 的图像向左平移
的图像向左平移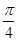 个单位,再向上平移
个单位,再向上平移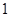 个单位,所得图像的解析式是
个单位,所得图像的解析式是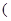
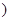
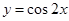
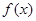 的最小正周期及在区间
的最小正周期及在区间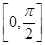
 上的最大值和最小值;
上的最大值和最小值;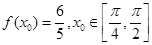 ,求
,求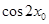 的值。
的值。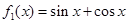 ,且
,且
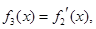
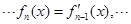
 ,则
,则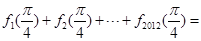
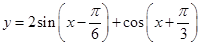 的一条对称轴是( )
的一条对称轴是( )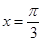

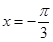
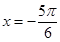
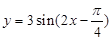 的图像,只需将函数
的图像,只需将函数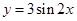 的图像向 平移 个单位.
的图像向 平移 个单位.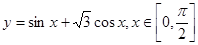 的单调递增区间__________
的单调递增区间__________