题目内容
若函数y=f(x)是函数y=ax(0<a≠1)的反函数,其图象经过点( ,a),则函数y=f(x+
,a),则函数y=f(x+ -3)的值域为 .
-3)的值域为 .
【答案】分析:先利用求反函数的方法得出原函数的反函数,结合其图象经过点( ,a)求出a值,最后利用对数函数的性质结合基本不等式即可求得函数y=f(x+
,a)求出a值,最后利用对数函数的性质结合基本不等式即可求得函数y=f(x+ -3)的值域.
-3)的值域.
解答:解:函数y=f(x)是函数y=ax(0<a≠1)的反函数是:
y=logax,
∵其图象经过点( ,a),
,a),
∴loga =a,⇒a=
=a,⇒a= ,
,
函数y=f(x+ -3)=
-3)= (x+
(x+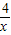 -3)
-3)
∵x+ -3≥2
-3≥2
∴ (x+
(x+ -3)≤0.
-3)≤0.
则函数y=f(x+ -3)的值域为:(-∞,0]
-3)的值域为:(-∞,0]
故答案为:(-∞,0].
点评:求反函数,一般应分以下步骤:(1)由已知解析式y=f(x)反求出x=Ф(y);(2)交换x=Ф(y)中x、y的位置;(3)求出反函数的定义域(一般可通过求原函数的值域的方法求反函数的定义域).
 ,a)求出a值,最后利用对数函数的性质结合基本不等式即可求得函数y=f(x+
,a)求出a值,最后利用对数函数的性质结合基本不等式即可求得函数y=f(x+ -3)的值域.
-3)的值域.解答:解:函数y=f(x)是函数y=ax(0<a≠1)的反函数是:
y=logax,
∵其图象经过点(
 ,a),
,a),∴loga
 =a,⇒a=
=a,⇒a= ,
,函数y=f(x+
 -3)=
-3)= (x+
(x+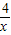 -3)
-3)∵x+
 -3≥2
-3≥2
∴
 (x+
(x+ -3)≤0.
-3)≤0.则函数y=f(x+
 -3)的值域为:(-∞,0]
-3)的值域为:(-∞,0]故答案为:(-∞,0].
点评:求反函数,一般应分以下步骤:(1)由已知解析式y=f(x)反求出x=Ф(y);(2)交换x=Ф(y)中x、y的位置;(3)求出反函数的定义域(一般可通过求原函数的值域的方法求反函数的定义域).

练习册系列答案
相关题目