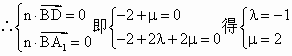题目内容
| |||||||||||||||
解析:
(1) |
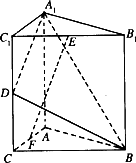
解:∵A1B1C1-ABC为直三棱住∴CC1⊥底面ABC∴CC1⊥BC ∵AC⊥CB∴BC⊥平面A1C1CA………………2分 ∴BC长度即为B点到平面A1C1CA的距离 ∵BC=2∴点B到平面A1C1CA的距离为2……………………4分 |
(2) |
解法一: 分别延长AC,A1D交于G.过C作CM⊥A1G于M,连结BM ∵BC⊥平面ACC1A1∴CM为BM在平面A1C1CA的内射影 ∴BM⊥A1G∴∠GMB为二面角B—A1D—A的平面角……………………6分 平面A1C1CA中,C1C=CA=2,D为C1C的中点 ∴CG=2,DC=1在直角三角形CDG中, 即二面角B—A1D—A的大小为
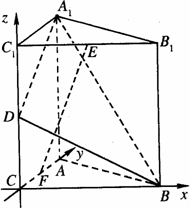
解法二: ∵A1B1C1—ABC为直三棱住C1C=CB=CA=2 AC⊥CBD、E分别为C1C、B1C1的中点 建立如图所示的坐标系得 C(0,0,0)B(2,0,0)A(0,2,0) C1(0,0,2)B1(2,0,2)A1(0,2,2) D(0,0,1)E(1,0,2)………………6分
平面ACC1A1的法向量为m=(1,0,0) 即二面角B—A1D—A的大小为 |
(3) |
解法一: 在线段AC上存在一点F,使得EF⊥平面A1BD………………10分 其位置为AC中点,证明如下………………11分 ∵A1B1C1—ABC为直三棱柱∴B1C1//BC ∵由(1)BC⊥平面A1C1CA,∴B1C1⊥平面A1C1CA ∵EF在平面A1C1CA内的射影为C1F∵F为AC中点∴C1F⊥A1D∴EF⊥A1D………13分 同理可证EF⊥BD∴EF⊥平面A1BD…………………14分 ∵E为定点,平面A1BD为定平面∴点F唯一 解法二: 在线段AC上存在一点F,设F(0,y,0)使得EF⊥平面A1BD……11分 欲使EF⊥平面A1BD由(2)知,当且仅当n//
即点F为AC中点………………14分 |

 阅读快车系列答案
阅读快车系列答案
| |||||||||||