题目内容
【题目】已知不等式x2+mx+3≤0的解集为A=[1,n],集合B={x|x2﹣ax+a≤0}.
(1)求m﹣n的值;
(2)若A∪B=A,求a的取值范围.
【答案】
(1)解:∵不等式x2+mx+3≤0的解集为A=[1,n],
∴ ![]() ,∴m=﹣4,n=3,
,∴m=﹣4,n=3,
∴m﹣n=﹣7;
(2)解:A∪B=A,∴BA.
①B=,△=a2﹣4a<0,∴0<a<4;
②B≠,设f(x)=x2﹣ax+a,则 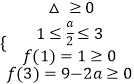 ,∴4≤a≤
,∴4≤a≤ ![]() ,
,
综上所述,0<a≤ ![]() .
.
【解析】本题考查的是集合的运算性质A∪B=A,BA.尤其是当B=的时候以及一元二次不等式代入特殊值的解法。
【考点精析】关于本题考查的解一元二次不等式,需要了解求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能得出正确答案.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能得出正确答案.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目