题目内容
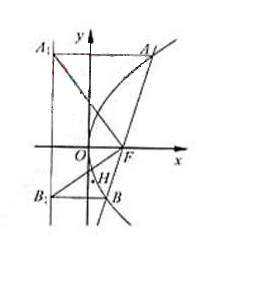
抛物线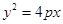 (p>0)的准线与x轴交于M点,过点M作直线l交抛物线于A、B两点.
(p>0)的准线与x轴交于M点,过点M作直线l交抛物线于A、B两点.
(1)若线段AB的垂直平分线交x轴于N(x0,0),比较x0与3p大小;
(2)若直线l的斜率依次为p,p2,p3,…,线段AB的垂直平分线与x轴的交点依次为N1,N2,N3,…,求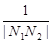 +
+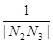 +…+
+…+ 的值.
的值.
【答案】
解:设直线l方程为y=k(x+p),代入y2=4px.
得k2x2+(2k2p-4p)x+k2p2=0.Δ=4(k2p-2p)2-4k2·k2p2>0,得0<k2<1.
令A(x1,y1)、B(x2,y2),则x1+x2=-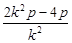 ,y1+y2=k(x1+x2+2p)=
,y1+y2=k(x1+x2+2p)=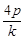 ,
,
AB中点坐标为(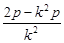 ,
,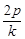 ).AB垂直平分线为y-
).AB垂直平分线为y-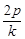 =-
=-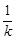 (x-
(x-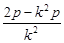 ).
).
令y=0,得x0=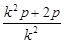 =p+
=p+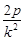 .由上可知0<k2<1,∴x0>p+2p=3p.∴x0>3p.
.由上可知0<k2<1,∴x0>p+2p=3p.∴x0>3p.
(2)解:∵l的斜率依次为p,p2,p3,…时,AB中垂线与x轴交点依次为N1,N2,N3,….
∴点Nn的坐标为(p+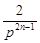 ,0).
,0).
|NnNn+1|=|(p+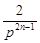 )-(p+
)-(p+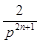 )|=
)|=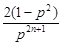 ,
,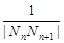 =
=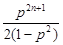 ,
,
所求的值为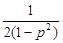 [p3+p4+…+p21]=
[p3+p4+…+p21]= ,因为0<k2<1,所以0<P<1
,因为0<k2<1,所以0<P<1
【解析】略

练习册系列答案
相关题目
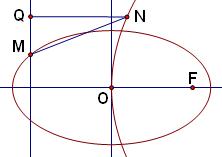
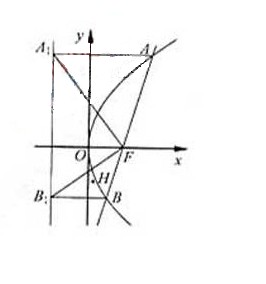
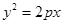 (p >0)的焦点F恰好是双曲线C2:
(p >0)的焦点F恰好是双曲线C2: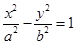 (a>0,b >0)的右焦点,且它们的交点的连线过点F,则双曲线的离心率为
(a>0,b >0)的右焦点,且它们的交点的连线过点F,则双曲线的离心率为 B.
B.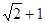 C.
C.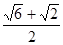 D.
D.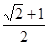
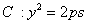 (p>0)
(p>0)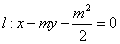 上。
上。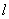 与抛物线C交于A、B,△A
与抛物线C交于A、B,△A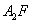 ,△
,△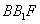 的重心分别为G,H
的重心分别为G,H