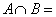题目内容
[番茄花园1] 已知m是非零实数,抛物线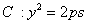 (p>0)
(p>0)
的焦点F在直线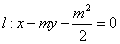 上。
上。
(I)若m=2,求抛物线C的方程
(II)设直线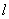 与抛物线C交于A、B,△A
与抛物线C交于A、B,△A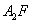 ,△
,△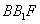 的重心分别为G,H
的重心分别为G,H
求证:对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外。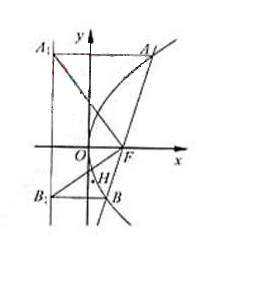
[番茄花园1]1.
【答案】
[番茄花园1] .解析:本题主要考查抛物线几何性质,直线与抛物线、点与圆的位置关系等基础知识,同时考查解析几何的基本思想方法和运算求解能力。
(Ⅰ)解:因为焦点F(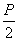 ,0)在直线l上,
,0)在直线l上,
得
又m=2,故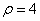
所以抛物线C的方程为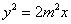
设A(x1,y1) , B(x2,y2)
由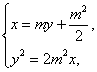 消去x得
消去x得
ym3y-m4=0,
由于m≠0,故 =4m6+4m4>0,
=4m6+4m4>0,
且有y1+y2=2m3,y1y2=-m4,
设M1,M2分别为线段AA1,BB1的中点,
由于2
可知G(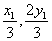 ),H(
),H(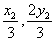 ),
),
所以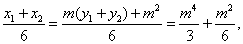
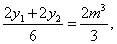
所以GH的中点M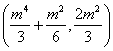 .
.
设R是以线段GH为直径的圆的半径,
则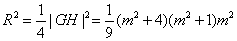
设抛物线的标准线与x轴交点N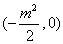 ,
,
则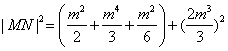
=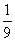 m4(m4+8 m2+4)
m4(m4+8 m2+4)
=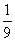 m4[(m2+1)(
m2+4)+3m2]
m4[(m2+1)(
m2+4)+3m2]
>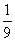 m2
(m2+1)( m2+4)=R2.
m2
(m2+1)( m2+4)=R2.
故N在以线段GH为直径的圆外.
[番茄花园1]22.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
[番茄花园1] 已知函数f(x)= 若a,b,c均不相等,且f(a)= f(b)= f(c),则abc的取值范围是
若a,b,c均不相等,且f(a)= f(b)= f(c),则abc的取值范围是
(A)(1,10) (B)(5,6) (C)(10,12) (D)(20,24)
二填空题:本大题共4小题,每小题5分。
[番茄花园1]1.
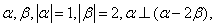 则
则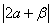 的值是 。
的值是 。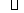 ABCD的三个顶点为A(-1,2),B(3,4),C(4,-2),点(x,y)在
ABCD的三个顶点为A(-1,2),B(3,4),C(4,-2),点(x,y)在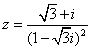 ,则
,则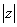 =
=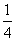 (B)
(B)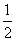 (C)1
(D)2
(C)1
(D)2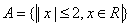 },
},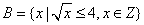 ,则
,则