题目内容
【题目】为了解高三学生的“理科综合”成绩是否与性别有关,某校课外学习兴趣小组在本地区高三年级理科班中随机抽取男、女学生各100名,然后对这200名学生在一次联合模拟考试中的“理科综合”成绩进行统计规定:分数不小于240分为“优秀”小于240分为“非优秀”.
(1)根据题意,填写下面的2×2列联表,并根据列联表判断是否有90%以上的把握认为“理科综合”成绩是否优秀与性别有关.
性别 | 优秀 | 非优秀 | 总计 |
男生 | 35 | ||
女生 | 75 | ||
总计 |
(2)用分层抽样的方法从成绩优秀的学生中随机抽取12名学生,然后再从这12名学生中抽取3名参加某高校举办的自主招生考试,设抽到的3名学生中女生的人数为X,求X的分布列及数学期望.
附: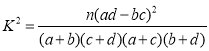 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)见解析,没有![]() 以上的把握认为“理科综合”成绩是否优秀与性别有关;
以上的把握认为“理科综合”成绩是否优秀与性别有关;
(2)见解析,![]()
【解析】
(1)根据题意填写列联表,计算观测值,对照临界值得出结论;
(2)用分层抽样法求出抽取的男、女生人数,知X的可能取值,
计算对应的概率值,写出X的分布列,求出数学期望值.
(1)根据题意,填写2×2列联表如下;
性别 | 优秀 | 非优秀 | 总计 |
男生 | 35 | 65 | 100 |
女生 | 25 | 75 | 100 |
总计 | 60 | 140 | 200 |
计算![]() ,且
,且![]() ,
,
所以没有![]() 以上的把握认为“理科综合”成绩是否优秀与性别有关;
以上的把握认为“理科综合”成绩是否优秀与性别有关;
(2)用分层抽样的方法从成绩优秀的学生中随机抽取12名学生,
男生有7人,女生有5人,从这12名学生中抽取3人,
抽到的3人中女生的人数为X,则X的可能取值为0,1,2,3;
计算![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
所以X的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
数学期望为![]()

 名校课堂系列答案
名校课堂系列答案【题目】工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标![]() 进行检测,一共抽取了
进行检测,一共抽取了![]() 件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标
件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标![]() 有关,具体见下表.
有关,具体见下表.
质量指标 |
|
|
|
频数 |
|
|
|
一年内所需维护次数 |
|
|
|
(1)以每个区间的中点值作为每组指标的代表,用上述样本数据估计该厂产品的质量指标![]() 的平均值(保留两位小数);
的平均值(保留两位小数);
(2)用分层抽样的方法从上述样本中先抽取![]() 件产品,再从
件产品,再从![]() 件产品中随机抽取
件产品中随机抽取![]() 件产品,求这
件产品,求这![]() 件产品的指标
件产品的指标![]() 都在
都在内的概率;
(3)已知该厂产品的维护费用为![]() 元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加
元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加![]() 元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这
元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这![]() 件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
