题目内容

函数f（x）=log₃x+x-3的零点一定在区间

A.
（0，1）
B.
（1，2）
C.
（2，3）
D.
（3，4）

C
分析：确定函数的定义域为（0，+∞）与单调性，再利用零点存在定理，即可得到结论．
解答：函数的定义域为（0，+∞）
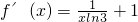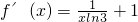求导函数，可得 $\text{[math]}$ ＞0，所以函数在（0，+∞）上单调增
∵f（2）=log₃2+2-3＜0，f（3）=log₃3+3-3＞0
∴函数f（x）=log₃x+x-3的零点一定在区间（2，3）
故选C．
点评：本题考查函数的单调性，考查零点存在定理，属于基础题．

练习册系列答案

B卷狂练系列答案

易考100一考通系列答案

伴你学江苏系列答案

启航新课堂系列答案

随堂小考系列答案

成才之路高中新课程学习指导系列答案

同步轻松练习系列答案

课课通课程标准思维方法与能力训练系列答案

钟书金牌教材金练系列答案

名牌学校分层课课练系列答案

相关题目

5、设函数f（x）=log_αx（a＞0）且a≠1，若f（x₁•x₂…x₁₀）=50，则f（x₁²）+f（x₂²）+…f（x₁₀²）等于（　　）

已知函数f（x）=log -

（x²-ax+3a）在[2，+∞）上是减函数，则实数a的范围是（　　）

A、（-∞，4]

C、（0，12）

已知函数f（x）=log 2(x2-x-2)
（1）求f（x）的定义域；
（2）当x∈[3，4]时，求f（x）的值域．

设有三个命题：“①0＜

＜1．②函数f（x）=log

x是减函数．③当0＜a＜1时，函数f（x）=log_ax是减函数”．当它们构成三段论时，其“小前提”是

（填序号）．

（2013•茂名二模）设函数f（x）的定义域为D，若存在非零实数l使得对于任意x∈M（M⊆D），有x+l∈D，且f（x+l）≥f（x），则称f（x）为M上的高调函数．现给出下列命题：
①函数f（x）=log

x为（0，+∞）上的高调函数；
②函数f（x）=sinx为R上的高调函数；
③如果定义域为[-1，+∞）的函数f（x）=x²为[-1，+∞）上的高调函数，那么实数m的取值范围是[2，+∞）；
其中正确的命题的个数是（　　）